
题目列表(包括答案和解析)
(本题满分10分)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
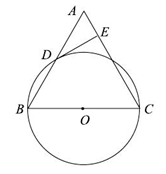
1.(1)求证:点D是AB的中点;
2.(2)判断DE与⊙O的位置关系,并证明你的结论;
3.(3)若⊙O的半径为9,AB=12,求DE的长.
(本题满分10分)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.

1.(1)求证:点D是AB的中点;
2.(2)判断DE与⊙O的位置关系,并证明你的结论;
3.(3)若⊙O的半径为9,AB=12,求DE的长.

 “构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.
“构造法”是一种重要方法,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的想象、灵活的构思.应用构造法解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行组合.| 5 |
| 10 |
| 13 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 5a |
| 2a |
| 17a |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com