
题目列表(包括答案和解析)
将一图形绕着点O顺时针方向旋转70°后,再绕着点O逆时针方向旋转120°,这时如果要使图形回到原来的位置,需要将图形绕着点O
A.顺时针方向旋转50°
B.逆时针方向旋转50°
C.顺时针方向旋转190°
D.逆时针方向旋转190°
将一图形绕着点P顺时针方向旋转50°后,再绕着点P逆时针方向旋转150°,这时如果要使图形回到原来的位置,需要将图形绕着点P按什么方向旋转的角度是( ).
A
.顺时针方向100° B.逆时针方向50°C
.顺时针方向200° D.逆时针方向100°图1是边长分别为![]() 和3的两个等边三角形纸片ABC和
和3的两个等边三角形纸片ABC和![]() 叠放在一起(C与
叠放在一起(C与![]() 重合).
重合).
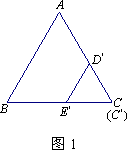
(1)固定△ABC,将△![]() 绕点C顺时针旋转30°得到△CDE,连结AD、BE(如图2).此时线段BE与AD有怎样的数量关系?并证明你的结论;
绕点C顺时针旋转30°得到△CDE,连结AD、BE(如图2).此时线段BE与AD有怎样的数量关系?并证明你的结论;
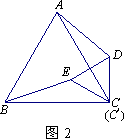
(2)设图2中CE的延长线交AB于F,并将图2中的△CDE在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△QRP(如图3).设△QRP移动(点P、Q在线段CF上)的时间为x秒,若△QRP与△AFC重叠部分的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围;
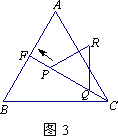
(3)若固定图1中的△![]() ,将△ABC沿
,将△ABC沿![]() 方向平移,使顶点C落在
方向平移,使顶点C落在![]() 的中点处,再以点C为中心顺时针旋转一定角度,设
的中点处,再以点C为中心顺时针旋转一定角度,设![]() ,边BC交
,边BC交![]() 于点M,边AC交
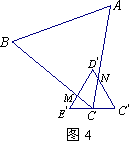
于点M,边AC交![]() 于点N(如图4).此时线段
于点N(如图4).此时线段![]() 的值是否随α的变化而变化?如果没有变化,请你求出
的值是否随α的变化而变化?如果没有变化,请你求出![]() 的值;如果有变化,请你说明理由.
的值;如果有变化,请你说明理由.
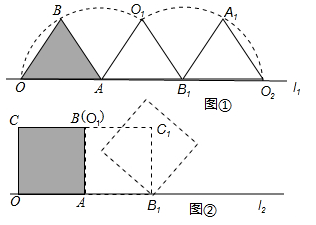
如图①.小意同学把一个正三角形纸片(即△OAB)放在直线l1上,OA边与直线11重合.然后将三角形纸片绕着顶点 A按顺时针方向旋转120°,此时点O运动到了点O1 处,点 B运动到了点B1处;小慧又将三角形纸片 AO1B1 绕B, 点按顺时针方向旋转120°点A运动到了点A1处. 点O1运动到了点O2 处(即顶点O经过上述两次旋转到达O2 处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2顶点O所经过的路程是这两圆弧的长度之和,并且这两端圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1 O1O2的面积之和.
小意进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线12 上,OA边与直线l2 重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°.此时点O运动到了点O1处(即点B处),点C运动到了点C1 处,点B运动到了点B1处;小意又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°……,按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片OABC按上述方法经过3次旋转.求顶点0经过的路程,并求顶点O在此运动过程中所形成的图形与直线12 围成图形的面积;若正方形OABC按上述方法经过5 次旋转,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是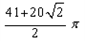 请你解答上述两个问题
请你解答上述两个问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com