
题目列表(包括答案和解析)
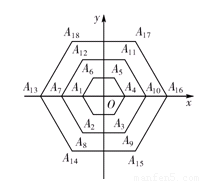
如图16,从内到外,边长依次为2,4,6,8,…的所有正六边形的中心均在坐标原点,且一组对边与x轴平行,它们的顶点依次用A1、A2、A3、A4、A5、A6、A7、A8、A9、A10、A11、A12……表示,那么顶点A62的坐标是 .
|
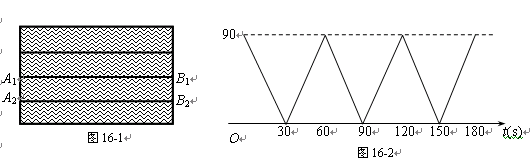
1.赛道的长度是_________m,甲船的速度是________m/s;
2.分别求出甲船在0≤t≤30和30<t≤60时,y关于t的函数关系式;
3.求出乙船由B2到达A2的时间,并在图16-2中画出乙船在3 分钟内的函数图象
4.请你根据(3)中所画的图象直接判断,若从甲、乙两船同时开始出发到3分钟为止,甲、乙共相遇了几次?
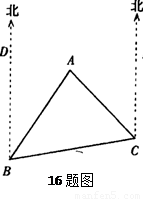
如图16,A岛在B岛的北偏东30°方向,C岛在B岛的北偏东80°方向,A岛在C岛北偏西40°方向.从A岛看B、C两岛的视角∠BAC是____.
如图16,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点.
三点.
(1)求过![]() 三点抛物线的解析式并求出顶点
三点抛物线的解析式并求出顶点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)试探究在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的周长最小,若存在,求出
的周长最小,若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

(7分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
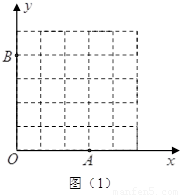
(2)如图16(1),已知格点(小正方形的顶点)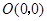 ,
,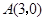 ,
,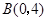 ,请你画出
,请你画出
以格点为顶点,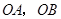 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形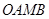 ;
;
 |
(3)如图16(2),将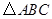 绕顶点
绕顶点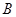 按顺时针方向旋转
按顺时针方向旋转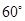 ,得到
,得到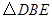 ,连结
,连结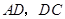 ,
,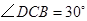 .求证:
.求证: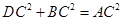 ,即四边形
,即四边形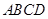 是勾股四边形
是勾股四边形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com