
题目列表(包括答案和解析)
某校对全校200名初三学生进行数学学习情况的测试, 并从中随机抽取了40份试卷, 下表是这40份试卷中填空题部分(共14小题, 每小题做对得3分、做错得0分)的答题情况:
| 答对题数 | 9 | 10 | 11 | 12 | 13 | 14 |
| 份数 | 1 | 1 | 3 | 8 | 15 | 12 |
根据所给信息, 填空:
(1) 这40份试卷中答对题数的平均数为_____________,中位数为________________;
(2) 由此可估计全校200名初三学生填空题部分的平均得分约为_____________分,得分率约为_________%,全部做对的约为_________人,答对题数的中位数约是___________.
填空题(每小题3分,共30分)
已知x-y=2,则x2-2xy+y2=________.

 ⑵
⑵
计算题(每小题5分,共10分)
① 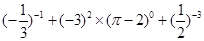
② 已知 ,求代数式
,求代数式 的值.
的值.
计算题(每小题5分,共10分)
① 
② 已知 ,求代数式
,求代数式 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com