
题目列表(包括答案和解析)
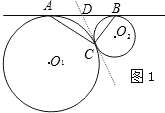 阅读下列材料:
阅读下列材料: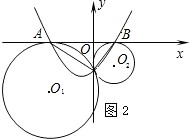
| 1 |
| 2 |
| 1 |
| 2 |

 23、如图,已知AB∥CD,求证:∠B+∠BEC-∠C=180度.
23、如图,已知AB∥CD,求证:∠B+∠BEC-∠C=180度.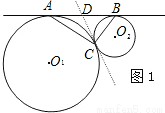
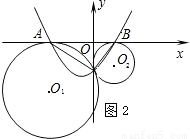
如右图,E、D分别是AB、AC上的一点,∠EBC、∠BCD的角平分线交于点M,∠BED、∠EDC的角平分线交于N.
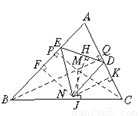
求证:A、M、N在一条直线上.
证明:过点N作NF⊥AB,NH⊥ED,NK⊥AC
过点M作MJ⊥BC,MP⊥AB,MQ⊥AC
∵EN平分∠BED,DN平分∠EDC
∴NF__________NH,NH__________NK
∴NF__________NK
∴N在∠A的平分线上
又∵BM平分∠ABC,CM平分∠ACB
∴__________=__________,__________=__________
∴__________=__________
∴M在∠A的__________上
∴M、N都在∠A的__________上
∴A、M、N在一条直线上
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com