
题目列表(包括答案和解析)
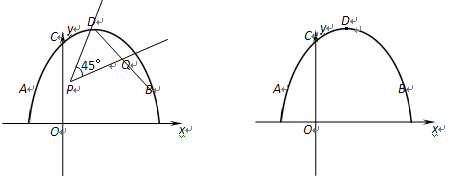
如图,抛物线![]() 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB = 2OC= 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB = 2OC= 3.
(1)求a,b的值;
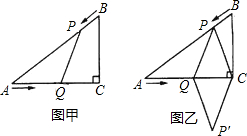
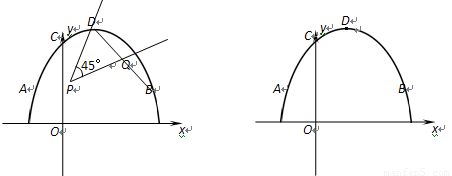
(2)将45°角的顶点P在线段OB上滑动(不与点B重合),该角的一边过点D,另一边与BD交于点Q,设P(x,0),y2=![]() DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式;
(3)在同一平面直角坐标系中,两条直线x = m,x = m+![]() 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为![]() ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由.
【解析】通过B(3,0),C(0,![]() )两点,求出拋物线的解析式,
)两点,求出拋物线的解析式,
(2)作DN⊥AB,由y1求出AB=4,DN=BN=2,DB=2![]() ,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ∽ △MBP,所以kPD2=DQ´DB=
,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ∽ △MBP,所以kPD2=DQ´DB=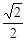 y2´2
y2´2![]() ,由j、k得y2与x的函数关系式
,由j、k得y2与x的函数关系式
(3)假设E、F、H、G围成四边形的面积能为![]() ,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,
,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,
通过四边形EFHG的面积求出m的值
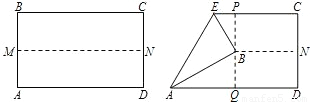
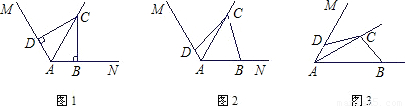
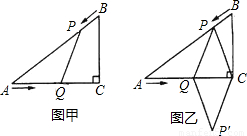
如图,抛物线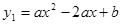 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB = 2OC= 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB = 2OC= 3.
(1)求a,b的值;
(2)将45°角的顶点P在线段OB上滑动(不与点B重合),该角的一边过点D,另一边与BD交于点Q,设P(x,0),y2=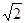 DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式;
(3)在同一平面直角坐标系中,两条直线x = m,x = m+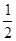 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为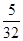 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由.
【解析】通过B(3,0),C(0,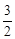 )两点,求出拋物线的解析式,
)两点,求出拋物线的解析式,
(2)作DN⊥AB,由y1求出AB=4,DN=BN=2,DB=2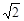 ,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ
∽ △MBP,所以kPD2=DQ´DB=
,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ
∽ △MBP,所以kPD2=DQ´DB=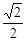 y2´2
y2´2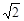 ,由j、k得y2与x的函数关系式
,由j、k得y2与x的函数关系式
(3)假设E、F、H、G围成四边形的面积能为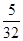 ,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,
,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,
通过四边形EFHG的面积求出m的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com