感知：利用图形中面积的等量关系可以得到某些数学公式．例如，根据图①甲，我们可以得到两数和的平方公式：，根据图①乙能得到的数学公式是                  ．

拓展：图②是由四个完全相同的直角三角形拼成的一个大正方形，直角三角形的两直角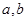边长为，，斜边长为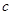，利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式，这个公式是：               ，这就是著名的勾股定理．请利用图②证明勾股定理．
应用：我国古代数学家赵爽的“勾股圆方图”是由四个完全相同的直角三角形与中间的一个小正方形拼成一个大正方形（如图③所示）．如果大正方形的面积是17，小正方形的面积是1，直角三角形的两直角边长分别为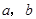，那么的值是         ．

“勾股弦”后人概括为“勾3、股4、弦5．”
（1）观察：3、4、5；5、12、13；7、24、25；…，发现这几组勾股数的勾都是奇数，且从3起就没有间断过，计算（9-1），（9+1）；（25-1），（25+1）；并根据你发现的规律，分别写出能表示7、24、25这一组数的股与弦的算式．
（2）根据（1）的规律，若用n（n为奇数，且n≥3）来表示所有这些勾股数的勾，请直接用n的代数式来表示它们的股和弦．
（3）继续观察：4、3、5；6、8、10；8、15、17；…，发现各组的第一个数都是偶数，且从4起也没有间断过．利用类似上述探索的方法，若用m（m为偶数，且m≥4）来表示所有这些勾股数的勾，请分别用m的代数式来表示它们的股和弦．

如果一个点能与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点．同样，点D也是A，B两点的勾股点．

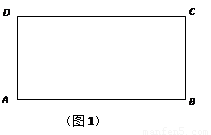
（1）如图1，矩形ABCD中，AB＝2，BC＝1，请在边CD上作出A，B两点的勾股点（点C和点D除外）（要求：尺规作图，保留作图痕迹，不要求写作法）；

（2 矩形ABCD中，AB＝3，BC＝1，直接写出边CD上A， B两点的勾股点的个数

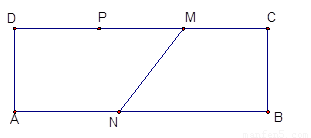
（3 如图2，矩形ABCD中，AB＝12，BC＝4，DP=4，DM＝8，AN＝5．过点P作直线l平行于BC，点H为M，N两点的勾股点，且点H在直线l上．求PH的长．

【解析】（1）以线段AB为直径的圆与线段CD的交点，或线段CD的中点；

（2）利用（1）中图形得出C，D，E，F即可得出答案；

（3）求出MN的长度，根据勾股数的特点得出符合要求的点