（1）如图1所示，在四边形ABCD中，AC=BD，AC与BD相交于点O，E，F分别是AD、BC的中点，连接EF，分别交AC、BD于点M，N，试判断△OMN的形状，并加以证明；（提示：利用三角形中位线定理）
（2）如图2，在四边形ABCD中，若AB=CD，E，F分别是AD、BC的中点，连接FE并延长，分别与BA，CD的延长线交于点M，N，请在图2中画图并观察，图中是否有相等的角？若有，请直接写出结论：；
（3）如图3，在△ABC中，AC＞AB，点D在AC上，AB=CD，E，F分别是AD、BC的中点，连接FE并延长，与BA的延长线交于点M，若∠FEC=45°，判断点M与以AD为直径的圆的位置关系，并简要说明理由．

如图1，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，分别与BA、CD的延长线交于点M、N，则∠BME=∠CNE（不需证明）．
（温馨提示：在图1中，连接BD，取BD的中点H，连接HE、HF，根据三角形中位线定理，证明HE=HF，从而∠1=∠2，再利用平行线性质，可证得∠BME=∠CNE．）
问题一：如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E、F分别是BC、AD的中点，连接EF，分别交DC、AB于点M、N，判断△OMN的形状，请直接写出结论；
问题二：如图3，在△ABC中，AC＞AB，D点在AC上，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于点G，若∠EFC=60°，连接GD，判断△AGD的形状并证明．

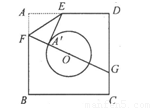
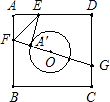如图，已知正方形纸片ABCD的边长为8，⊙O的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA恰好与⊙O相切于点A′（△EFA′与⊙O除切点外无重叠部分），延长FA′交CD边于点G，求A′G的长．

如图，已知正方形纸片ABCD的边长为8，⊙0的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA恰好与⊙O相切于点A ′(△EFA′与⊙O除切点外无重叠部分)，延长FA′交CD边于点G，则A′G的长是          ．