
题目列表(包括答案和解析)
| 1 |
| 2x |
| x+1 |
苏果超市经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,出售价格每涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(考查一元二次方程的应用)
(本小题满分5分)二次函数 中,自变量
中,自变量 与函数
与函数 的对
的对
| x | -1 | -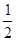 | 0 | 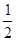 | 1 | 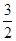 | 2 |  | 3 | |
| y | -2 | - | 1 |  | 2 |  | 1 | - | -2 |
 的两个根
的两个根 的取值范围是下
的取值范围是下 ②
②
 ④
④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com