(本题12分) 如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=，直线y=经过点C，交y轴于点G,且∠AGO=30°。

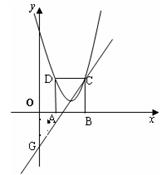
（1）点C、D的坐标分别是C（       ），D（       ）；

（2）求顶点在直线y=上且经过点C、D的抛物线的解析式；

（3）将（2）中的抛物线沿直线y=平移，平移后的抛物线交y轴于点F，顶点为点E。平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。

(本题12分) 如图，在平面直角坐标系中，二次函数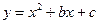的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.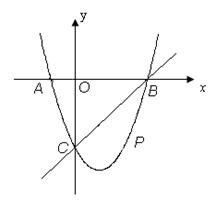

（1）求b,c的值．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形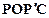， 那么是否存在点P，使四边形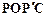为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积.

(本题12分) 如图，在平面直角坐标系中，二次函数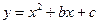的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.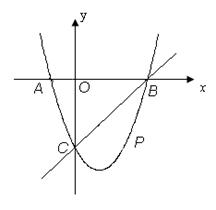

（1）求b,c的值．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形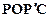，那么是否存在点P，使四边形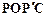为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积.

(本题12分)

如图，AD//BC，点E、F在BC上，∠1=∠2，AF⊥DE，垂足为点O.

(1)求证:四边形AEFD是菱形；

(2)若BE=EF=FC，求∠BAD+∠ADC的度数；

(3)若BE=EF=FC，设AB = m，CD= n，求四边形ABCD的面积.