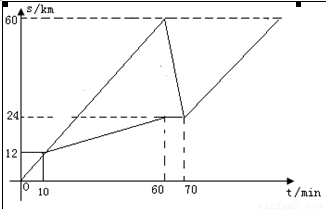
有六个学生分成甲、乙两组（每组三个人），分乘两辆出租车同时从学校出发去距学校60km的博物馆参观，10分钟后到达距离学校12km处有一辆汽车出现故障，接着正常行驶的一辆车先把第一批学生送到博物馆再回头接第二批学生，同时第二批学生步行12km后停下休息10分钟恰好与回头接他们的小汽车相遇，当第二批学生到达博物馆时，恰好已到原计划时间．设汽车载人速度、空载时的速度、学生步行速度分别是匀速的，汽车离开学校的路程s（千米）与汽车行驶时间t（分钟）之间的函数关系如图，假设学生上下车时间忽略不计．

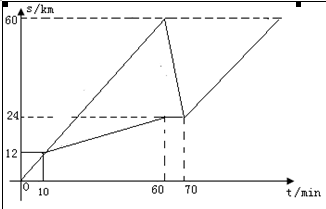
1.(1)原计划从学校出发到达博物馆的时间是　　▲   　分钟；

2.(2)求汽车在回头接第二批学生途中的速度；

3.(3)假设学生在步行途中不休息且步行速度每分钟减小0.04km，汽车载人时和空载时速度不变，问能否经过合理的安排，使得学生从学校出发全部到达目的地的时间比原计划时间早10分钟？如果能，请简要说出方案，并通过计算说明；如果不能，简要说明理由．

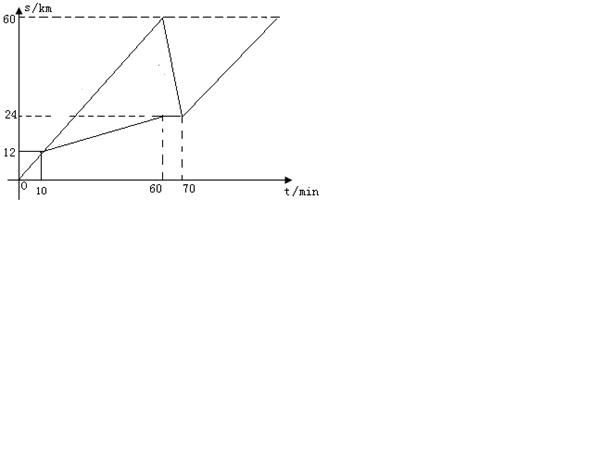
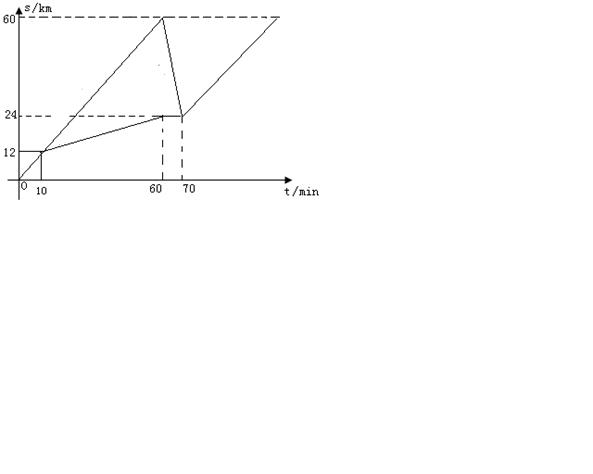
有六个学生分成甲、乙两组（每组三个人），分乘两辆出租车同时从学校出发去距学校60km的博物馆参观，10分钟后到达距离学校12km处有一辆汽车出现故障，接着正常行驶的一辆车先把第一批学生送到博物馆再回头接第二批学生，同时第二批学生步行12km后停下休息10分钟恰好与回头接他们的小汽车相遇，当第二批学生到达博物馆时，恰好已到原计划时间．设汽车载人速度、空载时的速度、学生步行速度分别是匀速的，汽车离开学校的路程s（千米）与汽车行驶时间t（分钟）之间的函数关系如图，假设学生上下车时间忽略不计．

1.(1)原计划从学校出发到达博物馆的时间是　　▲   　分钟；

2.(2)求汽车在回头接第二批学生途中的速度；

3.(3)假设学生在步行途中不休息且步行速度每分钟减小0.04km，汽车载人时和空载时速度不变，问能否经过合理的安排，使得学生从学校出发全部到达目的地的时间比原计划时间早10分钟？如果能，请简要说出方案，并通过计算说明；如果不能，简要说明理由．

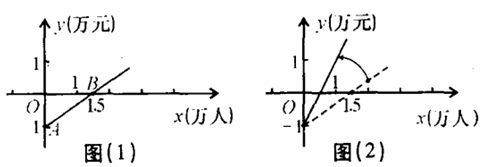
如图（ l ）是某公共汽车线路收支差额y(票价总收人减去运营成本）与乘客量 x 的函数图象．目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会.

乘客代表认为：公交公司应节约能源，改善管理，降低运营成本，以此举实现扭亏．

公交公司认为：运营成本难以下降，公司己尽力，提高票价才能扭亏．

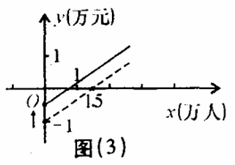
根据这两种意见，可以把图（ l ）分别改画成图（ 2 ）和图（ 3 ) ,

( l )说明图（ 1 ）中点 A 和点 B 的实际意义：

( 2 )你认为图（ 2 ）和图（ 3 ）两个图象中，反映乘客意见的是　　　　　　 　　　　　　，反映公交公司意见的是　　　　　　　　　　　　 　　　　　　.

( 3 ）如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢，请你在图（4）中画出符合这种办法的 y 与 x 的大致函数关系图象。