今年,重庆启动“两翼”农户万元增收工程,使农户纯收入在2009年的基础上户均增加1万元,某县种植了一种无公害蔬菜,该县决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元,随着补贴数额的不断增大,生产规模也不断增加,但每亩蔬菜的收益会相应降低.经调查,种植亩数y(亩)、每亩蔬菜的收益z(元)与补贴数额x(元)之间的关系如下表:
| x(元) |
0 |
100 |
200 |
300 |
… |
| y(亩) |
800 |
1600 |
2400 |
3200 |
… |
| z(元) |
3000 |
2700 |
2400 |
2100 |
… |
(1)分别求出政府补贴政策实施后种植亩数y、每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(2)要使全县这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值和此时种植亩数.
(3)在取得最大收益的情况下,为了满足市场需求,用不超过70亩的土地对这种蔬菜进行反季节的种植.为此需修建一些蔬菜大棚,修建大棚要用的支架、塑料膜等材料平均每亩的为650元,此外还要购置喷灌设备,这项费用(元)与大棚面积(亩)的平方成正比例,比例系数为25.这样,修建大棚后的这部分土地每亩的平均收益比没修前增加了2000元,在扣除修建费后总共增加了85000元.求修建了多少亩蔬菜大棚?(结果精确到个位,参考数据:
≈1.414)

 ,其中
,其中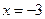 .
. ,其中
,其中 .
.