（2013年广东梅州8分）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．

（1）求线段EC的长；

（2）求图中阴影部分的面积．

（2013年广东梅州3分）从上面看如图所示的几何体，得到的图形是【    】

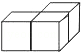
A．       B．      C．       D．

（2013年广东梅州10分）如图，已知抛物线y=2x²﹣2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．

（1）写出以A，B，C为顶点的三角形面积；

（2）过点E（0，6）且与x轴平行的直线l₁与抛物线相交于M、N两点（点M在点N的左侧），以MN为一边，抛物线上的任一点P为另一顶点做平行四边形，当平行四边形的面积为8时，求出点P的坐标；

（3）过点D（m，0）（其中m＞1）且与x轴垂直的直线l₂上有一点Q（点Q在第一象限），使得以Q，D，B为顶点的三角形和以B，C，O为顶点的三角形相似，求线段QD的长（用含m的代数式表示）．

（2013年广东梅州11分）用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

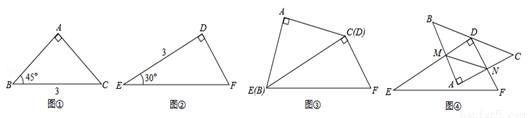
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．

（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；

（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数．

探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．

（2013年广东梅州3分）﹣3的相反数是　  　．