
题目列表(包括答案和解析)
 几何计算题:
几何计算题:
| DE | BE |
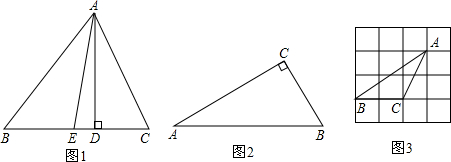
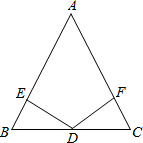 如图DE⊥AB,DF⊥AC,垂足分别为E、F,请你从(1)AB=AC;(2)BD=CD;(3)DE=DF中选出两个作为已知条件,另一个作为结论,编写一个几何证明题并完成证明过程.
如图DE⊥AB,DF⊥AC,垂足分别为E、F,请你从(1)AB=AC;(2)BD=CD;(3)DE=DF中选出两个作为已知条件,另一个作为结论,编写一个几何证明题并完成证明过程.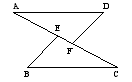
学科内知识综合题:
已知∠A是锐角,且tanA、cotA是关于x的一元二次方程![]() =0的两个实数根.
=0的两个实数根.
(1)求k的值;
(2)问∠A能否等于45°?请说明你的理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com