题目列表(包括答案和解析)
①直接开平方法：对于一元二次方程x2＝a（a≥0），因为x是a的平方根，所以x＝___________，即x1＝___________，x2＝___________，这种解一元二次方程的方法叫做直接开平方法．
②配方法：将一元二次方程ax2＋bx＋c＝0（a≠0）配成___________的形式后，当b2－4ac___________时，用直接开平方法求出它的根，这种解一元二次方程的方法叫做配方法．
③公式法：应用一元二次方程ax2＋bx＋c＝0（a≠0）的求根公式x＝___________(b2－4ac≥0)，这种解一元二次方程的方法叫做公式法．
④因式分解法：若一元二次方程ax2＋bx＋c＝0（a≠0）的左边是关于x的二次三项式易于分解成两个关于x的一次因式乘积的形式时，则方程ax2＋bx＋c＝0可变形为___________，分别令两个一次因式等于0，得两个关于x的一次方程___________和___________，通过解这两个一次方程，就可得原方程的解．这种解一元二次方程的方法叫做因式分解法．
关于x的一元二次方程－x2＋bx＋c＝0的两个实数根是m，4，其中0＜m＜4．
(1)求b，c的值；(用含m的代数式表示)
(2)如下图所示，设抛物线y＝－x2＋bx＋c与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，设点D(0，－2)，且AD2＋BD2＝25，求抛物线的解析式及点C的坐标；
(3)在(2)中所得的抛物线上是否存在点P，使得PC＝PD？若存在，求出P点坐标；若不存在，请说明理由．
(4)在(2)中所得的抛物线上是否存在点P，使得△PCD是等腰三角形？若存在，指出满足条件的P点的个数；若不存在，请说明理由．
已知关于x的一元二次方程－x2＋bx＋c＝0的两个实数根是m，4，其中0＜m＜4．
(1)求b，c的值(用含m的代数式表示)；
(2)设抛物线y＝－x2＋bx＋c与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，如图所示，若点D的坐标为(0，－2)，且AD2＋BD2＝25，求抛物线的关系式及点C的坐标；
(3)在(2)中所得的抛物线上是否存在点P，使得PC＝PD？若存在，求出P点的坐标；若不存在，请说明理由；
(4)在(2)中所得的抛物线上是否存在点P，使得△PCD是等腰三角形？若存在，指出满足条件的P点的个数；若不存在，请说明理由．
已知二次函数y＝ax2＋bx＋c(a≠0)的顶点坐标(－1，－
)及部分图象(如图所示)，由图象可知关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1＝1和x2＝________．
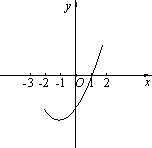
已知关于x的一元二次方程x2＋(2m－1)x＋m2＝0有两个实数根x1和x2．
(1)求实数m的取值范围；
(2)当
时，求m的值．
(友情提示：若x1，x2是一元二次方程ax2＋bx＋c＝0(a≠0)两根，则有
，
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com