练习册

  • 练习册
  • 试题
    计算:-32＝ A.9 B.-9 C. D.- 【查看更多】

     

    题目列表(包括答案和解析)

    有20箱橘子，以每箱25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下；

    ①20箱橘子中，最重的一箱比最轻的一箱多重多少千克？

    ②与标准重量比较，20箱橘子总计超过或不足多少千克？

    ③若橘子每千克售价2.6元，则出售这20箱橘子可卖多少元？(结果保留整数)

    (2)探索规律：

    观察下面由组成的图案和算式，解答问题：

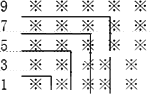
    1＋3＝4＝22

    1＋3＋5＝9＝32

    1＋3＋5＋7＋9＝25＝52

    ①请猜想1＋3＋5＋7＋9＋…＋19＝________；

    ②请猜想1＋3＋5＋7＋9＋…＋(2n－1＋＋(2n＋1)＋(2n＋3)＝________

    查看答案和解析>>

    通过计算比较下列各组数中两个数的大小，在空格中填写“＞”、“＜”、“＝”号：

    (1)12________21，23________32，34________43，45________54，56________65；

    (2)从第(1)小题的结果中通过归纳可以猜想nn+1与(n＋1)n的大小关系是________；

    (3)根据上面的归纳猜想得到的一般结论，你认为20032004与20042003谁大谁小？

    查看答案和解析>>

    先阅读下列短文，再解决后面的问题．

    3123是一个很大的数，怎样求出它的末位数字呢？

    我们依次计算一下31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187，38＝6561，……观察其末位数字的变化，寻找其中的规律，从而用归纳的方法得出结论：它们的末位数字不断循环出现3、9、7、1，周期为4．于是将指数123表示成30×4＋3，得出3123和33的末位数字是相同的结论，即3123的末位数字为7．

    (1)运用上面得出的规律，分别说出23123，123123，19931994，19932001的末尾数字是几？

    (2)当m是怎样的多位数时，mn(n为正整数)的末位数字是不变的？

    (3)运用上面的方法求出19941995，19981999，19972001的末位数字．

    查看答案和解析>>

    如图，小红家的阳台上放置了一个晒衣架．如图是晒衣架的(一端的横截面)侧面示意图，立杆AB、CD相交于点O，B、D两点立于地面，经测量：AB＝CD＝136 cm，OA＝OC＝51 cm，OE＝OF＝34 cm，现将晒衣架完全稳固张开，扣链EF成一条线段，且EF＝32 cm．

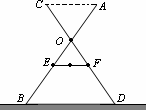
    (1)求证：AC∥BD；

    (2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°)；

    (3)小红的连衣裙穿在衣架后的总长度达到122 cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．

    (参考数据：sin61.9°≈0.882，cos61.9°≈0.471，tan28.1°≈0.533；可使用科学计算器．)

    查看答案和解析>>

    你能比较与的大小吗？

    为了解决这个问题，我们首先写出它的一般形式，即比较与的大小（n是正整数），然后我们从分析n=1，n=2，n=3……中发现规律，经归纳、猜想得出结论

    （1）通过计算，比较下列各组中两数的大小：（在横线上填写“＞”“＝”“＜”）

    ①12  21，②23   32；③34   43；④45   54；⑤56   65

    （2）从第（1）题的结果中，经过归纳，可以猜想出与（n+1）n的大小关系是   

    （3）根据以上归纳．猜想得到的一般结论，试比较下列两数的大小：与

     

    查看答案和解析>>


    同步练习册答案