（本小题满分10分）
观察控究，完成证明和填空．
如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．

【小题1】（1）求证：四边形EFGH是平行四边形；
【小题2】（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：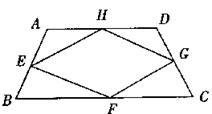

当四边形ABCD变成平行四边形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成矩形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成菱形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成正方形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
【小题3】（3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？

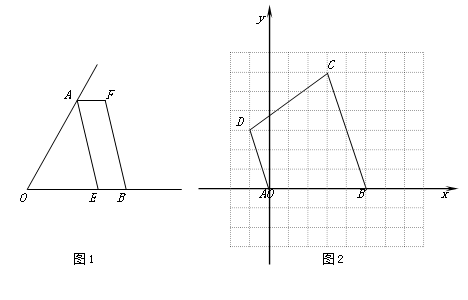
（本题满分10分）（1）如图1，已知∠AOB，OA＝OB，点E在OB边上，四边形AEBF 是平行四边形，请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不要求写作法）

（2）如图2，在10×10的正方形网格中，点A（0，0）、B（5，0）、C（3，6）、D（－1，3），

①依次连结A、B、C、D四点得到四边形ABCD，四边形ABCD的形状是    ▲     .

②在x轴上找一点P，使得△PCD的周长最短（直接画出图形，不要求写作法）；

此时，点P的坐标为     ▲     ，最短周长为     ▲     .

（本题满分10分）（1）如图1，已知∠AOB，OA＝OB，点E在OB边上，四边形AEBF是平行四边形，请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不要求写作法）
（2）如图2，在10×10的正方形网格中，点A（0，0）、B（5，0）、C（3，6）、D（－1，3），
①依次连结A、B、C、D四点得到四边形ABCD，四边形ABCD的形状是    ▲     .
②在x轴上找一点P，使得△PCD的周长最短（直接画出图形，不要求写作法）；
此时，点P的坐标为    ▲     ，最短周长为    ▲     .