(本题10分)
如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC=∠ABC，D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．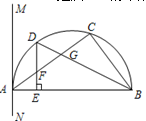

（1）求证：MN是半圆的切线；
（2）求证：FD=FG；
（3）若△DFG的面积为4.5，且DG=3，GC=4，试求△BCG的面积．

(本题10分) 如图,由边长为1的25个小正方形组成的正方形网格上有一个△ABC,请在网格上,按要求作出三角形，使它的三个顶点都落在小正方形的顶点上.(不要求写作法)
【小题1】（１）在甲图中作出△ＡＢＣ关于直线m的轴对称图形.

【小题2】（２）在乙图中作一个和△ABC相似但不全等的△DEF，并直接写出△DEF的面积为          .

（本题10分）如图所示的一块地，∠ADC=90°，AD=3m，CD=4m，AB=13m，BC=12m，求这块地的面积。

（本题10分）解不等式组，并求其整数解．

课题学习(本题10分)

●探究   (1) 在图1中，已知线段AB，CD，其中点分别为E，F．

①若A (-1，0)，B (3，0)，则E点坐标为__________；

②若C (-2，2)，D (-2，-1)，则F点坐标为__________；

(2)在图2中，已知线段AB的端点坐标为A(a，b) ，B(c，d)，求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．

●归纳  无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A(a，b)，B(c，d)，AB中点为D(x，y) 时，x=_________，y=___________．（不必证明）

★●运用 在图2中，的图象x轴交于P点。一次函数与的图象交点为A，B．

①求出交点A，B的坐标（用k表示）；

②若D为AB中点，且PD垂直于AB时，请利用上面的结论求出k的值。