
题目列表(包括答案和解析)
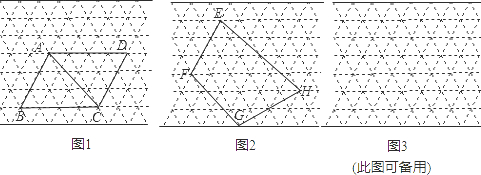

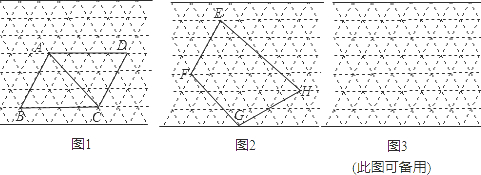
(2005·吉林)所图中的虚线网格我们称之为正三角形网格,它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)直接写出单位正三角形的高与面积;
(2)图a中的□ABCD含有多少个单位正三角形?□ABCD的面积是多少?
(3)求出图a中线段AC的长(可作辅助线);
(4)求出图b中四边形EFGH的面积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com