解直角三角形在生产.生活中有着广泛的应用.这就要求我们能从实际问题出发去分析.抽象.构建直角三角形模型．例4 如图4.公路PQ和公路PN在P处交汇.∠QPN=30°.点A处有一所中学.AP=16——青夏教育精英家教网—

解直角三角形在生产.生活中有着广泛的应用.这就要求我们能从实际问题出发去分析.抽象.构建直角三角形模型．例4 如图4.公路PQ和公路PN在P处交汇.∠QPN=30°.点A处有一所中学.AP=160m.设拖拉机行驶时.周围100m以内会受噪音影响.那么拖拉机在公路PN上由P向N方向行驶时.学校是否会受噪音的影响?设拖拉机的速度为18km/s.如果有影响.那么影响的时间是多长? 分析:学校是否会受影响.取决于点A到PN的距离与100m的长短的比较．解:过点A作AB⊥PN.垂足为B.因为∠NPQ=30°. 所以AB=(m)<100m．所以学校会受影响．设拖拉机行至C处时学校刚受影响. 超过D处时不在受影响.则AC=AD=100(m). 在Rt△ABC中.BC=. 同理BD=60.所以CD=120．所以学校受影响的时间为t=．同角三角函数的基本关系三角函数角 sin cos tan 300 450 1 600 从表中不难得出: . . . 那么.对于任意锐角A.是否存在.呢? 事实上.同角三角函数之间.具有三个基本关系: 如图.在.所对的边依次为a.b.c 则 ① ②. ③ 证明:① 即 ② 即 . ③ 即通过以上证明.可以得出以下结论: ①对于任意锐角A.的正弦与余弦的平方和等于1.即． ②对于任意锐角A.的正弦与余弦的商等于的正切.即． ③对于任意锐角A.的余弦与正弦的商等于的余切.即． ④对于任意锐角A.的正切和余切互为倒数.．运用以上关系.在计算.解题的过程中.可以简化计算过程．例1 已知为锐角.求．解:为锐角又此题还可以利用定义求解.方法不唯一．例2 计算解:原式= =1-1 =0 本题也可直接把特殊角的三角函数值代入计算.但过程较为复杂.同学们了解了同角三角函数之间的基本关系.不仿试解下面的题目．1．化简: 【查看更多】

题目列表(包括答案和解析)

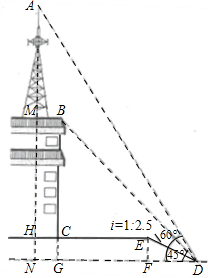小鹏学完解直角三角形知识后，给同桌小艳出了一道题：“如图所示，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上，已知α=36°，求长方形卡片的周长．”请你帮小艳解答这道题．（精确到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

查看答案和解析>>

（2012•遂宁）小明在数学课中学习了《解直角三角形》的内容后，双休日组织教学兴趣小组的小伙伴进行实地测量．如图，他们在坡度是i=1：2.5的斜坡DE的D处，测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°，斜坡高EF=2米，CE=13米，CH=2米．大家根据所学知识很快计算出了铁塔高AM．亲爱的同学们，相信你也能计算出铁塔AM的高度！请你写出解答过程．（数据

≈1.41，

≈1.73供选用，结果保留整数）

查看答案和解析>>

小鹏学完解直角三角形知识后，给同桌小艳出了一道题：“如图所示，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上，已知α=36°，则长方形卡片的周

长为

mm．”（精确到1mm）
（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

查看答案和解析>>

甲、乙两位学生为了将解直角三角形的知识学以致用，他们相约到孙文公园测量孙中山塑像及其底座的高度．下面是两位同学的一段对话：
甲：我站在此处看塔顶仰角为45°，乙：我站在此处看塔顶仰角为30°．
甲：我们的身高都是1.6m，乙：我们相距4m．
请你根据两位同学的对话，计算孙中山塑像及其底座的高度大致是多少？（精确到0.1米，

≈1.73）．

查看答案和解析>>

根据下列条件，解直角三角形：
（1）在Rt△ABC中，∠C=90°，a=8，∠B=60°；
（2）在Rt△ABC中，∠C=90°，∠A=45°，b=

．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学