某玩具厂生产某种玩具，无法确定颜色，该厂厂长的儿子小勇自告奋勇担当了调查员的角色．他访问了阳光幼儿园里两班共50名小朋友各自喜爱的颜色，记录如图所示1．

(1)请你完成上表中的其他数据．

(2)小勇调查提供的数据，可否成为厂家确定生产玩具颜色的依据？

(3)该玩具厂就该种玩具的颜色随机调查了5000名幼儿园小朋友，并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率，绘制了下面的表2．随着调查次数的增加，红色的频率是如何变化的？你能估计调查到10000名同学时，红色的频率是多少吗？

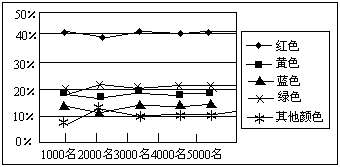
(4)你认为该厂在生产玩具时，对玩具的颜色应如何安排？

某厂生产某种零件，每个零件的成本为40元，出厂单价为60元，该厂为鼓励销售商订购，制定了促销条件：当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元．
（1）若销售商一次订购x（x＞100）个零件，直接写出零件的实际出厂单价y（元）？
（2）设销售商一次订购x（x＞100）个零件时，工厂获得的利润为W元（W＞0）．
①求出W（元）与x（个）之间的函数关系式及自变量x的取值范围；并算出销售商一次订购多少个零件时，厂家可获得利润6000元；
②厂家为了达到既鼓励销售商订购又保证自己能获取最大利润的目的，重新制定新促销条件：在原有的基础上又增加了限制条件--销售商订购的全部零件的实际出厂单价不能低于a（元）．请你利用函数及其图象的性质求出a的值；并写出实行新促销条件时W（元）与x（个）之间的函数关系式及自变量x的取值范围．（工厂出售一个零件利润=实际出厂单价-每个零件的成本）