
题目列表(包括答案和解析)
、(本题12分) 如图甲,在△ABC中,E是AC边上的一点,
(1)在图甲中,作出以BE为对角线的平行四边形BDEF,使D、F分别在BC和AB边上;
(2)改变点E的位置,则图甲中所作的平行四边形BDEF有没有可能为菱形?若有,请在图乙中作出点E的位置(用尺规作图,并保留作图痕迹);若没有,请说明理由.
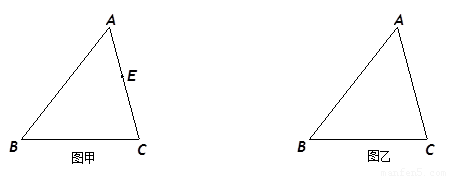 |
 元交费.
元交费.| 月份 | 用电量(度) | 交电费总额(元) |
| 10月份 | 45 | 10 |
| 11月份 | 80 | 25 |

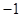 ,那么他告诉魔术师的结果应该是 ;
,那么他告诉魔术师的结果应该是 ;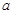 时,请按魔术师要求的运算过程写成代数式?
时,请按魔术师要求的运算过程写成代数式?﹣(本题12分)在一平直河岸 同侧有
同侧有 两个村庄,
两个村庄, 到
到 的距离分别是3km和2km,
的距离分别是3km和2km,
 .现计划在河岸
.现计划在河岸 上建一抽水站
上建一抽水站 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为 ,且
,且 (其中
(其中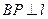 于点
于点 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为 ,且
,且 (其中点
(其中点 与点
与点 关于
关于 对称,
对称, 与
与 交于点
交于点 ).
).
 |
 km(用含
km(用含 的式子表示);
的式子表示); 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算, km(用含
km(用含 的式子表示).
的式子表示). 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); ②请你参考右边方框中的方法指导,
②请你参考右边方框中的方法指导, (当
(当 时)的所有取值情况进
时)的所有取值情况进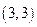 ,正方形ABCD的边长为1.
,正方形ABCD的边长为1.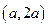 (B)
(B)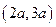 (C)
(C)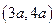 (D)
(D)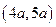
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com