练习册

  • 练习册
  • 试题
    如图Rt△ABC中∠C=.D在BC上.ABBE,EFBC 与F,且∠EAB=∠DAC 求证:CD=BF 【查看更多】

     

    题目列表(包括答案和解析)

    如图，甲、乙、丙、丁四位同学从四块全等的等腰直角三角形纸板上裁下四块不同的纸板（阴影部分），他们的具体裁法如下：甲同学：如图1所示裁下一个正方形，面积记为S1；乙同学：如图2所示裁下一个正方形，面积记为S2；丙同学：如图3所示裁下一个半圆，使半圆的直径在等腰Rt△的直角边上，面积记为S3；丁同学：如图所示裁下一个内切圆，面积记为S4则下列判断正确的是（　　）
    ①S1=S2；②S3=S4；③在S1，S2，S3，S4中，S2最小．
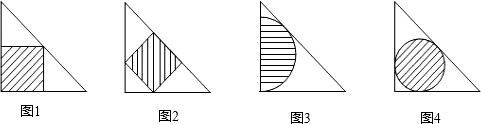
    精英家教网
    A、①②B、②③C、①③D、①②③

    查看答案和解析>>

    　　如图，Rt△ABO的顶点A是双曲线与直线在第二象限的交点，AB⊥轴于B，且。求这两个函数的解析式。

     

    查看答案和解析>>

    正弦定理

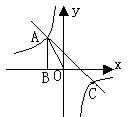
    　　命题：如图，在锐角△ABC中，BC＝a．CA＝b．AB＝c，△ABC的外接圆半径为R．则＝2R．

    　　证明：连接CO并延长交O于点D．连接DB．则∠D＝∠A．

    　　∵CD为O的直径，∴∠DBC＝．在Rt△DBC中

    　　∵sinD＝．∴sinA＝，即＝2R．

    　　同理＝2R．＝2R．

    　　∴＝2R．

    请你阅读前面所给的命题及其证明后，完成下面的(1)、(2)两小题：

    (1)前面的阅读材料中略去了＝2R和＝2R”的证明过程，请你把＝2R”的证明过程补写出来．

    (2)直接用前面阅读材料中命题的结论解题．

    已知：如图，在锐角△ABC中，BC＝，CA＝，∠A＝．求△ABC的外接圆半径R及∠C．

    　

    查看答案和解析>>

    利用切线性质证明等腰三角形

    　　如图，已知：如图(1)，AB是⊙O的直径，P是AB上的一点(与A、B不重合)．QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：

    　　证明：连结OC．

    　　∵OA＝OC，∴∠A＝∠1．

    　　∵CD切⊙O于C点，

    　　∴∠OCD＝90°，

    　　∴∠1＋∠2＝90°，

    　　∴∠A＋∠2＝90°．

    　　在Rt△QPA中，∠QPA＝90°，

    　　∴∠A＋∠Q＝90°，

    　　∴∠2＝∠Q．∴DQ＝DC．

    　　即△CDQ是等腰三角形．

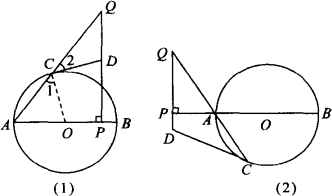
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图(2)所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    　　如图所示，在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点．

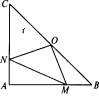
    　　①写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)；

     

    　　②如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM请判断△OMN的形状，并证明你的结论．

     

    查看答案和解析>>


    同步练习册答案