【阅读理解】:若一条直线l把一个图形分成面积相等的两个图形,则称这样的直线l叫做这个图形的等积直线.如图①,直线l经过三角形ABC的顶点A和边BC的中点N,易知直线l将△ABC分成两个面积相等的图形,则称直线l为△ABC的等积直线.

根据上述内容解决以下问题:
(1)如图②,在矩形ABCD中,直线l经过AD、BC边的中点M、N,请你判断直线l是否为该矩形的等积直线.
是
是
(填“是”或“否”)并在图②中再画出一条该矩形的等积直线;(不必写作法,保留作图痕迹)
(2)如图③,在梯形ABCD中,直线l经过AD、BC边的中点M、N,请你判断直线l是否为该梯形的等积直线.
是
是
;(填“是”或“否”)
(3)在图③中,过MN的中点O任做一条直线PQ分别交AD,BC于点P,Q(如图④),猜想PQ是否为该梯形的等积直线,若“是”请证明,若“不是”请说明理由;
【探索应用】:
李大爷家有一块五边形的土地如图⑤,已知∠A、∠B、∠C都是直角,AB∥CD,BC∥AE,现决定画一条线把五边形土地分为两
块,其中一块地用来改种核桃树,要求两块地面积相同,请你帮李大爷画出这条线,并判断这样的直线有多少条(保留作图痕迹,不必说明理由).

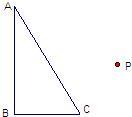 20、任画一个直角△ABC,其中∠B=90°,取△ABC外一点P为旋转中心,按逆时针方向旋转60°,作出旋转后的三角形.
20、任画一个直角△ABC,其中∠B=90°,取△ABC外一点P为旋转中心,按逆时针方向旋转60°,作出旋转后的三角形.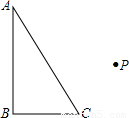
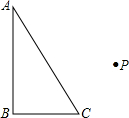 任画一个直角△ABC,其中∠B=90°,取△ABC外一点P为旋转中心,按逆时针方向旋转60°,作出旋转后的三角形.
任画一个直角△ABC,其中∠B=90°,取△ABC外一点P为旋转中心,按逆时针方向旋转60°,作出旋转后的三角形.

