练习册

  • 练习册
  • 试题
    如图10,在正方形的网格上有6个斜三角形:①,②,③,④,⑤,⑥.在② ⑥中.与三角形①相似的是 .. 图10 图11 【查看更多】

     

    题目列表(包括答案和解析)

    如图(1)是从长40 cm、宽30 cm的矩形钢板的左上角截取一块长为20 cm、宽为10 cm的矩形后剩下的一块下脚料．工人师傅要将它作适当切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能短的的正方形工件．

    李师傅的做法是：设新正方形的边长为x(x＞0)．依题意，割补前后图形的面积相等，有．由此可知正方形的边长等于两个直角边分别为30 cm和10 cm的直角三角形斜边的长．于是，画出如图(2)所示的正方形．

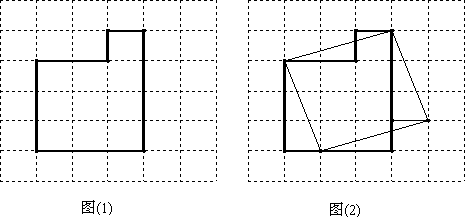
    请你仿照李师傅的做法，确定一个与李师傅方法不同的割补方法，在图(1)的正方形网格图(图中每个小正方形的边长均为10 cm)中用虚线画出拼接后的正方形，并在下面的横线上写出接缝的长．(不写分析过程和画法)

    解：接缝的长为________cm．

    查看答案和解析>>

    同学们，学习了无理数之后，我们已经把数的领域扩大到了实数的范围，这说明我们的知识越来越丰富了！可是，无理数究竟是一个什么样的数呢？下面让我们在几个具体的图形中认识一下无理数．
    （1）如图①△ABC是一个边长为2的等腰直角三角形．它的面积是2，把它沿着斜边的高线剪开拼成如图②的正方形ABCD，则这个正方形的面积也就等于正方形的面积即为2，则这个正方形的边长就是
    		2
    ，它是一个无理数．

    （2）如图，直径为1个单位长度的圆从原点O沿数轴向右滚动一周，圆上的一点P（滚动时与点O重合）由原点到达点O′，则OO′的长度就等于圆的周长π，所以数轴上点O′代表的实数就是
    π
    π
    ，它是一个无理数．

    （3）如图，在Rt△ABC中，∠C=90°，AC=2，BC=1，根据勾股定理可求得AB=
    		5
    		5
    ，它是一个无理数．

    好了，相信大家对无理数是不是有了更具体的认识了，那么你是也试着在图形中作出两个无理数吧：
    1、你能在6×8的网格图中（每个小正方形边长均为1），画出一条长为
    		10
    的线段吗？

    2、学习了实数后，我们知道数轴上的点与实数是一一对应的关系．那么你能在数轴上找到表示 -
    		5
    的点吗？

    查看答案和解析>>


    同步练习册答案