九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践--应用--探究的过程：
（1）实践：他们对一条公路上横截面为拋物线的单向双车道的隧道（如图①）进行测量，测得一隧道的路面宽为10m，隧道顶部最高处距地面6.25m，并画出了隧道截面图，建立了如图②所示的直角坐标系，请你求出抛物线的解析式．
（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖直方向上的高度差至少为0.5m．为了确保安全，问该隧道能否让最宽3m，最高3.5m的两辆厢式货车居中并列行驶（两车并列行驶时不考虑两车间的空隙）？
（3）探究：该课题学习小组为进一步探索抛物线的有关知识，他们借助上述拋物线模型，提出了以下两个问题，请予解答：
I．如图③，在抛物线内作矩形ABCD，使顶点C、D落在拋物线上，顶点A、B落在x轴 上．设矩形ABCD的周长为l求l的最大值．
II•如图④，过原点作一条y=x的直线OM，交抛物线于点M，交抛物线对称轴于点N，P 为直线0M上一动点，过P点作x轴的垂线交抛物线于点Q．问在直线OM上是否存在点P，使以P、N、Q为顶点的三角形是等腰直角三角形？若存在，请求出P点的坐标；若不存在，请说明理由．

九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践——应用——探究的过程

（1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量，测得隧道的路面宽为10米，隧道顶部最高处距地面6.25米，并画出了隧道截面图，建立了如图所示的直角坐标系，请你求出抛物线的解析式

（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖起方向上的高度差至少为0.5米，为了确保安全，问该隧道能否让最宽3米，最高3.5米的两辆车居中并列行驶（不考虑两车之间的空隙）？

（3）探究：该课题学习小组为进一步探究抛物线的有关知识，他们借助上述抛物线模型，提出了以下两个问题，请予解答：

①如图，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上，顶点A、B落在x轴上，设矩形ABCD的周长为为l，求l的最大值

②如图，过原点作一条直线y=x，交抛物线于M，交抛物线的对称轴于N，P为直线OM上一动点，过点P作x轴的垂线交抛物线于点Q，问在直线OM上是否存在点P，使以点P、N、Q为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由

 

 

 

 

 

 

 

 

 

九（1）班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践--应用--探究的过程：
（1）实践：他们对一条公路上横截面为拋物线的单向双车道的隧道（如图①）进行测量，测得一隧道的路面宽为10m，隧道顶部最高处距地面6.25m，并画出了隧道截面图，建立了如图②所示的直角坐标系，请你求出抛物线的解析式．
（2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖直方向上的高度差至少为0.5m．为了确保安全，问该隧道能否让最宽3m，最高3.5m的两辆厢式货车居中并列行驶（两车并列行驶时不考虑两车间的空隙）？
（3）探究：该课题学习小组为进一步探索抛物线的有关知识，他们借助上述拋物线模型，提出了以下两个问题，请予解答：
I．如图③，在抛物线内作矩形ABCD，使顶点C、D落在拋物线上，顶点A、B落在x轴 上．设矩形ABCD的周长为l求l的最大值．
II•如图④，过原点作一条y=x的直线OM，交抛物线于点M，交抛物线对称轴于点N，P 为直线0M上一动点，过P点作x轴的垂线交抛物线于点Q．问在直线OM上是否存在点P，使以P、N、Q为顶点的三角形是等腰直角三角形？若存在，请求出P点的坐标；若不存在，请说明理由．

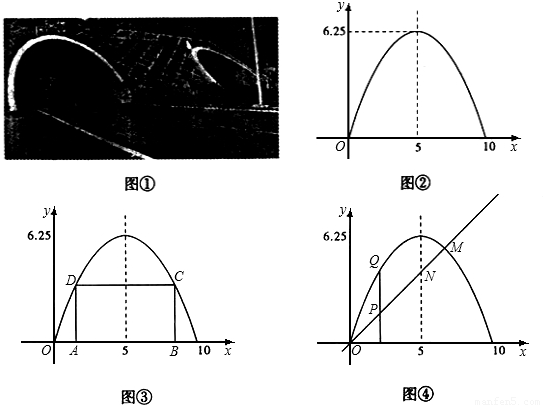
九(1)班数学课题学习小组，为了研究学习二次函数问题，他们经历了实践一应用——探究的过程：

  (1)实践：他们对一条公路上横截面为抛物线的单向双车道的隧道(如图①)进行测量，测得一隧道的路面宽为10m．隧道顶部最高处距地面6.25m，并画出了隧道截面图．建立了如图②所示的直角坐标系．请你求出抛物线的解析式．

  (2)应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖直方向上的高度差至少为0.5m．为了确保安全．问该隧道能否让最宽3m．最高3.5m的两辆厢式货车居中并列行驶(两车并列行驶时不考虑两车间的空隙)?

  (3)探究：该课题学习小组为进一步探索抛物线的有关知识，他们借助上述抛物线模型塑．提出了以下两个问题，请予解答：

Ⅰ．如图③，在抛物线内作矩形ABCD，使顶点C、D落在抛物线上．顶点A、B落在x轴上．设矩形ABCD的周长为，求的最大值。

Ⅱ．如图④，过原点作一条的直线OM，交抛物线于点M．交抛物线对称轴于点N，P为直线OM上一动点，过P点作x轴的垂线交抛物线于点Q。问在直线OM上是否存在点P，使以P、N、Q为顶点的三角形是等腰直角三角形？若存在，请求出P点的坐标；若不存在，请说明理由．