题目列表(包括答案和解析)
已知点E、F为抛物线
上的两点，过点E、F分别作
轴的垂线，分别交轴于点B、D，交直线
于点A、C，设S为直线AB、CD与轴、直线所围成图形的面积。
（1）当
，
，
时，计算：①当
，
时，求
、
、S；②当
，
时，求、、S；通过以上的计算，猜想S与－的数量关系；
（2）当抛物线在轴上方，且点
、
在抛物线的对称轴的同侧（点E在点F的左侧）时（如图1），（1）中的结论是否仍然成立?请说明你的判断；
（3）如果将（2）中的“同侧”改为“异侧”（如图2），其他条件不变，并设M为直线与轴交点，
，
，求
、
与、的数量关系（直接写出答案）。
如图，在△ABC中，∠BAC=90°， BC∥x轴，抛物线y=ax2－2ax＋3经过△ABC的三个顶点，并且与x轴交于点D、E，点A为抛物线的顶点．
（1）求抛物线的解析式；
（2）连接CD，在抛物线的对称轴上是否存在一点P使△PCD为直角三角形，若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
如图，直线y＝－x＋3与x轴、y轴分别相交于点B、点C，经过B、C两点的抛物线y＝ax2＋bx＋c与x轴的另一个交点为A，顶点为P，且对称轴是直线x＝2．
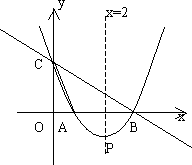
(1)求该抛物线的函数表达式；
(2)若点R在(1)中抛物线的对称轴上，且使得△RAC的周长最小，求点R的坐标；
(3)该Q为(1)中抛物线对称轴上一点，在抛物线上是否存在这样一点M，使得以A、B、Q、M为顶点的四边形是平行四边形．若存在，求出点M的坐标；若不存在，请说明理由．
下图，直线y＝－x＋3与x轴，y轴分别相交于点B，点C，经过B、C两点的抛物线y＝ax2＋bx＋c与x轴的另一交点为A，顶点为P，且对称轴是直线x＝2．
(1)求A点的坐标；
(2)求该抛物线的函数表达式；
(3)连结A、C，请问在x轴上是否存在点Q，使得以点P、B、Q为顶点的三角形与△ABC相似，若存在，请求出点Q的坐标；若不存在，请说明理由．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com