练习册

  • 练习册
  • 试题
    6．画出函数与的图象. (1)完成下表 -3 -2 -1 0 1 2 3 (2)建立平面直角坐标系.并在坐标系中做出二次函数与的图象. (3)抛物线与之间有什么关系?它们是轴对称图形吗?它们的对称轴和顶点坐标分别是什么? (4)随的增大分别是如何变化的? 思维拓展 【查看更多】

     

    题目列表(包括答案和解析)

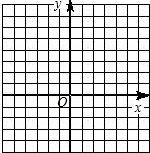
    在同一直角坐标系中分别画出函数与的图象，试用这两个图象说明何时x比大，何时x比小．

    查看答案和解析>>

    精英家教网已知：y1=（1-
    1k
    ）x+1（k≠0，1）y2=|x-1|
    （1）写出不论k为何值时，直线y1的图象都具有的2条性质；
    （2）利用列表、描点和连线的方法在给定的坐标系（小方格单位长度为1）中画出函数y2的图象；
    （3）如果函数y1、y2的图象有两个不同的交点，求出由这两个图象围成的图形面积（可用含k的式子表示）；
    （4）如果函数y1、y2的图象只有一个交点，写出y1与x轴交点坐标的最小值．

    查看答案和解析>>

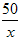    现有一水池，容积为50m3，如果每小时注水xm3，则经过yh可以注满，试写出y与x的函数关系式，并画出其图象，在解答此题时，合作学习小组的李明同学的解答过程是：函数关系式为y=，用描点法画出函数y=的图象，如图一所示。

    图一                             图二
    张旭同学的解答过程是：函数关系式为y=张旭同学的解答过程是：函数关系式为y=（x>0），用描点法画出函数y=（x>0）的图象，如图二所示，哪位同学的解答有错误？请讨论后指出存在的问题，并分析错误的原因．（x>0），用描点法画出函数y=（x>0）的图象，如右图所示，哪位同学的解答有错误？请讨论后指出存在的问题，并分析错误的原因．

    查看答案和解析>>

    某家电集团公司生产某种型号的新家电，前期投资200万元，每生产一台这种新家电，后期还需要其它投资0．3万元，已知每台新家电可实现产值0．5万元。

    (1)分别求总投资y1(万元)和总利润y2(万元)关于新家电的总产量z(台)的函数关系式，并画出函数y2的图象；

    (2)请你利用第(1)小题中的图象回答：当新家电的总产量为900台时，该公司是亏损还是盈利；

    (3)请你利用第(1)小题中y2与z的关系式，分析该公司的盈亏情况．

    (注：总投资=前期投资+后期其它投资，总利润=总产值一总投资)

    查看答案和解析>>

    已知：y1=（1-数学公式）x+1（k≠0，1）y2=|x-1|
    （1）写出不论k为何值时，直线y1的图象都具有的2条性质；
    （2）利用列表、描点和连线的方法在给定的坐标系（小方格单位长度为1）中画出函数y2的图象；
    （3）如果函数y1、y2的图象有两个不同的交点，求出由这两个图象围成的图形面积（可用含k的式子表示）；
    （4）如果函数y1、y2的图象只有一个交点，写出y1与x轴交点坐标的最小值．

    查看答案和解析>>


    同步练习册答案