练习册

  • 练习册
  • 试题
    可求出AB= 4米 ∵8＞4 ∴距离B点8米远的保护物不在危险区内 【查看更多】

     

    题目列表(包括答案和解析)

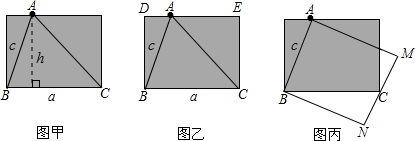
    现有可建造60米围墙的材料，准备依靠原有旧墙围成如图所示的仓库，墙长为a米，试问：

    ⑴a＝50，能否围成总面积为225米2的仓库？若能，AB的长为多少米？

    ⑵题中墙的长度a＞50米，能否用所给的材料围成一个面积最大的仓库？若能，求出AB的长，若不能，请说明理由。

    查看答案和解析>>

    学校生物园有一块空地是锐角△ABC的形状（如图甲），面积为100平方米，BC=a米，AB=c米，且a＞c．现在准备将这块空地扩建成矩形草坪，四周用栅栏围起来．现在有图乙、图丙两种方案．

    在图甲中，由S=
    1
    2
    ah=100可得ah=200，∵c＞h，∴ac＞200．
    （1）在图乙中，矩形BCED的面积为
    200
    200
    平方米，用矩形面积公式可以求出边BD的长为
    200
    a
    200
    a
    米．
    （2）在图丙中，矩形ABNM的面积为
    200
    200
    平方米，边BN的长为
    200
    c
    200
    c
    米．
    （3）在图乙、图丙两种方案中，哪种方案矩形的周长较大？说明理由．

    查看答案和解析>>

    某旅游胜地欲开发一座景观山．从山的侧面进行勘测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚（点C）的水平线为x轴、过山顶（点A）的铅垂线为y轴建立平面直角坐标系如图（单位：百米）．已知AB所在抛物线的解析式为y=-
    1
    4
    x2+8，BC所在抛物线的解析式为y=
    1
    4
    （x-8）2，且已知B（m，4）．
    （1）设P（x，y）是山坡线AB上任意一点，用y表示x，并求点B的坐标；
    （2）从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20厘米，长度因坡度的大小而定，但不得小于20厘米，每级台阶的两端点在坡面上（见图）．
    ①分别求出前三级台阶的长度（精确到厘米）；
    ②这种台阶不能一直铺到山脚，为什么？
    （3）在山坡上的700米高度（点D）处恰好有一小块平地，可以用来建造索道站．索道的起点选择在山脚水平线上的点E处，OE=1600（米）．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y=
    1
    28
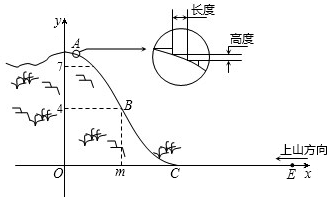    （x-16）2．精英家教网试求索道的最大悬空高度．

    查看答案和解析>>

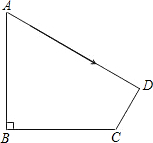    精英家教网为了给市民提供一个休闲健身的场所，市政府决定将一块矩形（如图）空地规划成休闲广场，初步规划AB为1200米，BC长为400米，后经测量发现，如果AB长每减少30米，则BC长就可增加20米，为了合理的利用土地，AB长又不能小于600米，设AB边的长为x米．矩形休闲广场的占地面积为S平方米．
    （1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）
    （2）当x为何值时，S有最大值？并求出最大值．
    （参考公式：二次函数y=ax2+bx+c（a≠0），当x=-
    b
    2a
    时，y最大（小）值=
    4ac-b2
    4a
    ）

    查看答案和解析>>

    精英家教网如图，小鹏准备测量学校旗杆的高度．他发现当斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面BC和斜坡坡面CD上，测得旗杆在水平地面上的影长BC=20米，在斜坡坡面上的影长CD=8米，太阳光线AD与水平地面成30°角，且太阳光线AD与斜坡坡面CD互相垂直．请你帮小鹏求出旗杆AB的高度（精确到1米）．（可供选用数据：取
    		2
    =1.4，
    		3
    =1.7）

    查看答案和解析>>


    同步练习册答案