（本题满分11分）如图，在梯形ABCD中，AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点，连接AF、FG，过点D作DE∥FG交AF于点E。

（1）求证：△AED≌△CGF；

（2）若梯形ABCD为直角梯形，∠B=90°，判断四边形DEFG是什么特殊四边形？并证明你的结论；

（3）若梯形ABCD的面积为a(平方单位），则四边形DEFG的面积为       （平方单位）。（只写结果，不必说理）

（本题满分12分，其中第（1）小题5分，第（2）小题7分）
已知：如图，在矩形ABCD中，点E、F分别在边AD、BC上，EF垂直平分AC，垂足为O，联结AF、CE．

（1）求证：四边形AFCE是菱形；
（2）点P在线段AC上，满足，求证：CD∥PE．

（本题满分12分，其中第（1）小题5分，第（2）小题7分）

已知：如图，在矩形ABCD中，点E、F分别在边AD、BC上，EF垂直平分AC，垂足为O，联结AF、CE．

（1）求证：四边形AFCE是菱形；

（2）点P在线段AC上，满足，求证：CD∥PE．

（本题满分12分）

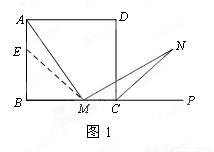
1.（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，

AB=BC．∴∠NMC=180°—∠AMN­—∠AMB=180°—∠B—∠AMB=∠MAB

=∠MAE．

（下面请你完成余下的证明过程）

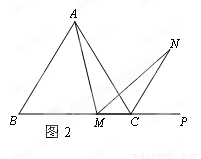
2.（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

3.（3）若将（1）中的“正方形ABCD”改为“正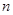边形ABCD…X”，请你作出猜想：当∠AMN=            °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）