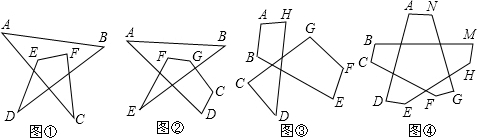
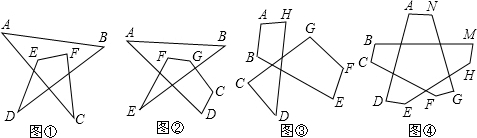
阅读材料:
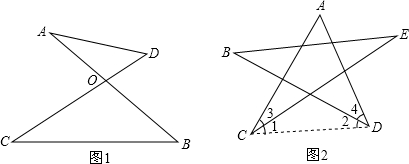
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F=
360°
360°
;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G=
540°
540°
;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
720°
720°
;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=
1080°
1080°
;
请你从图③或图④中任选一个,写出你的计算过程.