
题目列表(包括答案和解析)
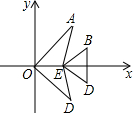 如图,若将图案中六个点的纵坐标不变,横坐标分别变成原来的4倍,连结各点所得图案与原图案相比( )
如图,若将图案中六个点的纵坐标不变,横坐标分别变成原来的4倍,连结各点所得图案与原图案相比( )| A、纵向拉长为原来的4倍 | ||
B、横向压缩为原来的
| ||
| C、横向拉长为原来的4倍 | ||
| D、横向拉长为原来的3倍 |

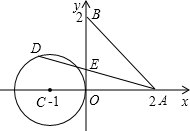 如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )| A、2 | ||||
| B、1 | ||||
C、2-
| ||||
D、2-
|
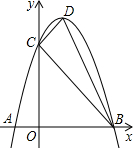 如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别相交于A(-1,0)、B(3,0)、C(0,3)三点,其顶点为D.(1)求:经过A、B、C三点的抛物线的解析式;
如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别相交于A(-1,0)、B(3,0)、C(0,3)三点,其顶点为D.(1)求:经过A、B、C三点的抛物线的解析式;| b |
| 2a |
| 4ac-b2 |
| 4a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com