
题目列表(包括答案和解析)
| x |
| x-1 |
| 2x-2 |
| x |
| x |
| x-1 |
| 2 |
| y |
| y-6 |
| y-6 |
| A、1个 | B、2个 | C、3个 | D、4个 |
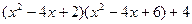 进行因式分解的过程.
进行因式分解的过程.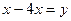
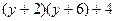 (第一步)
(第一步) (第二步)
(第二步)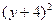 (第三步)
(第三步)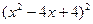 (第四步)
(第四步) 进行因式分解.
进行因式分解.下面是某同学对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
请问:
(1)该同学因式分解的结果是否彻底?____________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果____________________________
(2)请你模仿以上方法尝试对多项式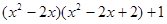 进行因式分解.
进行因式分解.
 +
+ +3=0,设
+3=0,设 =y,则原方程可化为y+
=y,则原方程可化为y+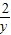 +3=0;
+3=0;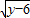 =0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+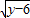
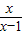 +
+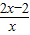 +3=0,设
+3=0,设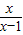 =y,则原方程可化为y+
=y,则原方程可化为y+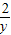 +3=0;
+3=0;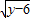 =0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+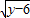
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com