练习册

  • 练习册
  • 试题
    1．填表: 直线与圆的 位置关系 图形 公共点 个数 公共点 名称 圆心到直线的距离d与圆的半径r的关系 直线的 名称 相交 相切 相离 【查看更多】

     

    题目列表(包括答案和解析)

    实践与应用：
    一个西瓜放在桌子上用刀切下去，一刀可以切成2块，2刀最多可以切成4块；3刀最多可以切成7块，4刀最多可以切成11块（如图）．
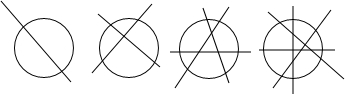
    精英家教网
    上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题，有没有规律呢？请先进行试验，然后回答以下问题．
    （1）填表：

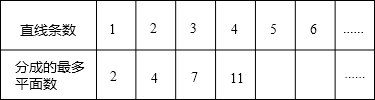
    精英家教网
    （2）设n条直线把平面最多分成的块数是S，请写出S关于n的表达式．（不需要解题过程）

    查看答案和解析>>

    27、在直角坐标系中，横、纵坐标都为整数的点叫做整点．设坐标轴的单位长为1厘为，整点P从原点O出发，速度为1厘米/秒，且点P只能向上或向右运动．
    请回答下列问题：
    （1）填表；
    （2）当点P从点O出发4秒时，可能得到的整点的坐标是：
    （4，0）（3，1）（2，2）（1，3）（0，4）
    ；
    （3）当点P从点O出发10秒时，可得到的整点个数是
    11
    个；
    （4）当点P从O点出发
    15
    秒时，可得到整点（10，5）；
    （5）当点P从点O出发30秒时，整点P恰好在直线y=2x-6上，请求P点坐标；
    （6）若设点P从点O出发的时间t（秒）时，可能得到的整点个数为n，试写出n与t之间的函数关系式，并写出t的取值范围．

    查看答案和解析>>

    （2013•吉林）如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=
    1
    4
    x2于点A、B，交抛物线C2：y=
    1
    9
    x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
    【猜想与证明】
    填表：
    m 1 2 3
    AB
    CD
    		       
         
    由上表猜想：对任意m（m＞0）均有
    AB
    CD
    =
    2
    3
    2
    3
    ．请证明你的猜想．
    【探究与应用】
    （1）利用上面的结论，可得△AOB与△CQD面积比为
    2
    3
    2
    3
    ；
    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
    【联想与拓展】
    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为
    8
    27
    8
    27
    ．

    查看答案和解析>>

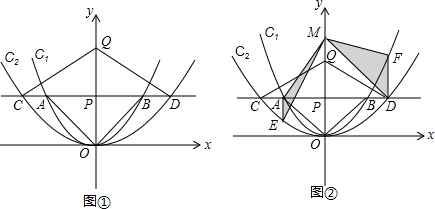
    如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=x2于点A、B，交抛物线C2：y=x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
    【猜想与证明】
    填表：
    m123
          
         
    由上表猜想：对任意m（m＞0）均有=______．请证明你的猜想．
    【探究与应用】
    （1）利用上面的结论，可得△AOB与△CQD面积比为______；
    （2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
    【联想与拓展】
    如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为______．

    查看答案和解析>>

    (1)填表：

    (2)已知一条抛物线的形状(开口方向和开口大小)与抛物线y＝2x2的相同，它的对称轴是直线x＝－2，且当x＝1时，y＝6，求这条抛物线的解析式．

    (3)定义：如果点P(t，t)在抛物线上，则点P叫做这条抛物线的不动点．

    ①求出(2)中所求抛物线的所有不动点的坐标；

    ②当a，b，c满足什么关系式时，抛物线y＝ax2＋bx＋c一定存在不动点？

    查看答案和解析>>


    同步练习册答案