
题目列表(包括答案和解析)
△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 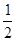 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
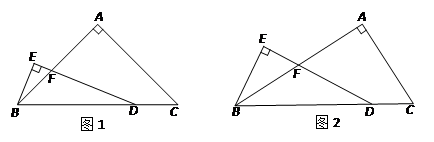
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
【解析】(1)根据平行线的性质和全等三角形求证,(2)由(1)的结论可以直接写出
△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 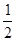 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
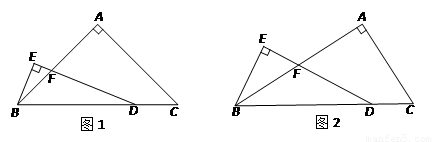
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
【解析】(1)根据平行线的性质和全等三角形求证,(2)由(1)的结论可以直接写出

问题:如图(12),在菱形![]() 和菱形
和菱形![]() 中,点
中,点![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .探究
.探究![]() 与
与![]() 的位置关系及
的位置关系及![]() 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.

请你参考小聪同学的思路,探究并解决下列问题:
1.若图(12)中![]() ,写出线段
,写出线段![]() 与
与![]() 的位置关系及
的位置关系及![]() 的值,并说明理由;
的值,并说明理由;
2.将图(12)中的菱形![]() 绕点
绕点![]() 顺时针旋转,使菱形
顺时针旋转,使菱形![]() 的对角线
的对角线![]() 恰好与菱形
恰好与菱形![]() 的边
的边![]() 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
3.若图(12)中![]() ,将菱形
,将菱形![]() 绕点
绕点![]() 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
解:(1)线段![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;![]() .
.
 和菱形
和菱形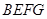 中,点
中,点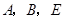 在同一条直线上,
在同一条直线上,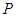 是线段
是线段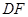 的中点,连结
的中点,连结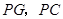 .探究
.探究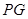 与
与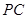 的位置关系及
的位置关系及 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长 交
交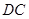 于点
于点 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.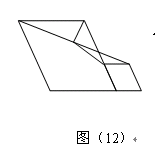
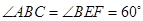 ,写出线段
,写出线段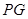 与
与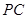 的位置关系及
的位置关系及 的值,并说明理由;
的值,并说明理由;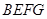 绕点
绕点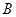 顺时针旋转,使菱形
顺时针旋转,使菱形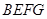 的对角线
的对角线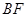 恰好与菱形
恰好与菱形 的边
的边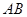 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.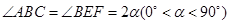 ,将菱形
,将菱形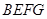 绕点
绕点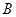 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出 的值(用含
的值(用含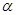 的式子表示).
的式子表示).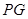 与
与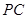 的位置关系是 ;
的位置关系是 ;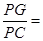 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com