练习册

  • 练习册
  • 试题
    如图14-1.一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动.将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转． (1)如图14-2.当EF与AB相交于点M.GF与BD相交于点N时.通过观察或测量BM.FN的长度.猜想BM.FN满足的数量关系.并证明你的猜想, (2)若三角尺GEF旋转到如图14-3所示的位置时.线段FE的延长线与AB的延长线相交于点M.线段BD的延长线与GF的延长线相交于点N.此时.(1)中的猜想还成立吗?若成立.请证明,若不成立.请说明理由． 湖北省襄樊市襄阳区峪山中学 毕保洪 张良坤 电话:13972273985 【查看更多】

     

    题目列表(包括答案和解析)

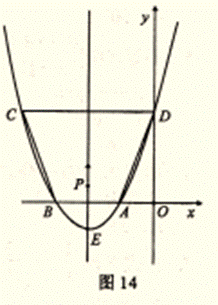
    如图14，已知抛物线 与x轴的一个交点A的坐标为（-1,0），对称轴为直线 x = 2.

    （1）求抛物线与x轴的另一个交点B的坐标；

    （2）点D是抛物线与y轴的交点，点C是抛物线上的另一点。已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式，并指出顶点E的坐标；

    （3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动。设点P运动的时间为t秒。

    ①当t为     秒是，△PAD的周长最小？当t为     秒时，△PAD是以AD为腰的等腰三角形？（结果保留根号）

           ②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由。

    查看答案和解析>>

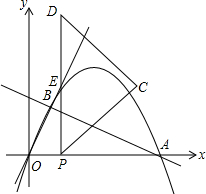    （2013•太仓市二模）如图，已知抛物线y=ax2+bx（a≠0）经过点A（10，0）和B（2，4），点P从原点出发向点A作匀速运动，速度为每秒1个单位，过点P作x轴的垂线，与直线OB交于点E，延长PE到D，使DE=PE，以PD为斜边在直线PD的右侧作等腰Rt△PCD．
    （1）a=
    -
    1
    4
    -
    1
    4
    ；b=
    5
    2
    5
    2
    ；
    （2）若点C恰好落在抛物线上，求点P运动的时间t；
    （3）若在点P运动的同时，线段OA上另一个点Q从点A出发向原点作匀速运动，速度为每秒2个单位（当点Q到达原点时运动即结束）．过点Q做x轴的垂线，与直线AB交于点F延长QF到点M，使得FM=QF，以QM为斜边，在QM的左侧作等腰Rt△QMN．求当两个等腰直角三角形恰好有一条边落在同一直线上时对应时刻t的值．

    查看答案和解析>>

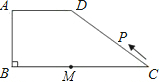    城市规划期间，欲拆除一电线杆AB（如图），已知与电线杆AB水平距离14米的D处有一等腰梯形大坝CDEF，该梯形的上底CF长为3米，下底DE长为5米，∠CDE=60°，在坝顶C处测得杆顶A的仰角为30°，D、G之间是宽3米的人行道．试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封闭？请说明理由．（在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域）精英家教网

    查看答案和解析>>

    精英家教网如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C?D?A?B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有
     
    个．

    查看答案和解析>>

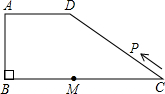    精英家教网如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C→D→A→B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有几个？并求出相应等腰三角形的腰长．

    查看答案和解析>>


    同步练习册答案