
题目列表(包括答案和解析)
(本题10分)
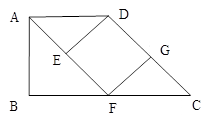
如图,梯形ABCD中,AD∥BC,BC=2AD,F、G分别为边BC、CD的中点,连接AF,FG,过D作DE∥GF交AF于点E。
1.(1)证明△AED≌△CGF
2.(2)若梯形ABCD为直角梯形,判断四边形DEFG是什么特殊四边形?并证明你的结论。
(本题10分)如图,梯形ABCD中,AD∥BC,BC=2AD,F、G分别为边BC、CD的中点,连接AF,FG,过D作DE∥GF交AF于点E。
(1)证明△AED≌△CGF
(2)若梯形ABCD为直角梯形,判断四边形DEFG是什么特殊四边形?并证明你的结论。
 |
(本题10分)已知,如图,△OAB中,OA=OB,⊙O经过AB的中点C,且与OA、OB分别交于点D、E.
1.(1) 如图①,判断直线AB与⊙O的位置关系并说明理由;
2.(2) 如图②,连接CD、CE,当△OAB满足什么条件时,四边形ODCE为菱形,并证明你的结论。

课题学习(本题10分)
●探究 (1) 在图1中,已知线段AB,CD,其中点分别为E,F.
①若A (-1,0), B (3,0),则E点坐标为__________;
②若C (-2,2), D (-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b) ,B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.
●归纳 无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d), AB中点为D( x,y) 时,x=_________,y=___________.(不必证明)
x,y) 时,x=_________,y=___________.(不必证明)
★●运用 在图2中,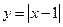 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数 与
与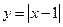 的图象交点为A,B.
的图象交点为A,B.
① 求出交点A
求出交点A ,B的坐标(用k表示);
,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值。

(本题10分)实验证明,平面镜的反射规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图①所示:∠1=∠2.
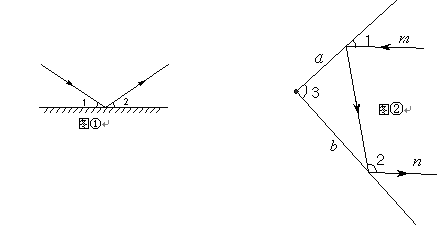
(1)如图②所示,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射.若被
反射.若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且∠1=50º,则∠2= º,∠3= º.
平行,且∠1=50º,则∠2= º,∠3= º.
(2)在图②中,若∠1变为55º、40º、30º时,∠3的度数是否发生变化?
(3)由(1)、(2)请你猜想:当平面镜![]() 、
、![]() 的夹角∠3= º时,可以使任何射到平面镜
的夹角∠3= º时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请你说明其中的道理.
平行.请你说明其中的道理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com