阅读下列证明过程：已知，如图四边形ABCD中，AB＝DC，AC＝BD，AD≠BC，求证：四边形ABCD是等腰梯形．

读后完成下列各小题．

(1)证明过程是否有错误？如有，错在第几步上，答：　　　　　　　　　　　　 　　　　　　　　　　　　 ．

(2)作DE∥AB的目的是：　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 ．

(3)有人认为第9步是多余的，你的看法呢？为什么？答：　　　　　　　　　　　　　　 　　　　　　　　　　　　　　．

(4)判断四边形ABED为平行四边形的依据是：　　　　　　　　　　　　 　　　　　　　　　　 ．

(5)判断四边形ABCD是等腰梯形的依据是　　　　　　　　　　　　 　　　　　　　　　　　　．

(6)若题设中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗？为什么？

答：　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　 ．

　　　　　　　　　　　　　　　　　　　　  D

　　　　　　　　　　　　　　　　　　　　  A　　　　　　　　    B

　　　　   　　　　　　　　　　　　　　　　　E   

如图所示，已知：四边形ABCD中，AB=DC、AC=BD、AD≠BC，求证：四边形ABCD是等腰梯形。

证明：过点D作DE∥AB，交BC于E，则∠ABE=∠1。　　　　　　  ①

∵AB=DC，AC=DB，BC=CB，

∴△ABC≌△DCB.　　　　　　　　 ②

∴∠ABC=∠DCB.　　　　　　　　  ③

∴∠1=∠DCB.　　　　　　　　    ④

∴AB=DC=DE。　　　　　　　　    ⑤

∴四边形ABED是平行四边形。　　 ⑥

∴AD∥BC，　　　　　　　　　　  ⑦

BE=AD.　　　　　　　　　　　　  ⑧

又∵AD≠BC，∴BE≠BC.

∴点E、C是不同的点，DC不平行AB. 　　　　   ⑨

又∵AB=CD，∴四边形ABCD是等腰梯形。　　　　 ⑩

读后完成下列各小题。

(1)证明过程是否有错误?如有错在第几步上。答：______________。

(2)作DE∥AB的目的是________________________。

(3)有人认为第9步是多余的，你的看法是______________。

(4)判断四边形ABED为平行四边形的依据是______________。

(5)判断四边形ABCD是等腰梯形的依据是______________。

(6)若题设中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗?你的意见是______________。

探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

(1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

（2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②

如图，BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C 

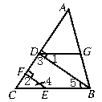
证明：∵BD⊥AC，EF⊥AC(　　  ) 

∴∠2=∠3=90° 

∴BD∥EF(　　　　　　　　　　　　  ) 

∴∠4=_____(　　　　　　　　　　　　　　　　    ) 

∵∠1=∠4(　　　　　　　　　　　　　　　　　　    ) 

∴∠1=_____(　　　　　　　　　　　　　　　　　　 ) 

∴DG∥BC(　　　　　　　　　　　　　　　　   ) 

∴∠ADG=∠C(　　　　　　　　　　　　　　　　   )