练习册

  • 练习册
  • 试题
    ⊙O与⊙O1交于A.B.O1在⊙O上.CD是过A点的割线交⊙O与⊙O1交于C.D.连BC交⊙O1于E.求证:AE∥BD. 【查看更多】

     

    题目列表(包括答案和解析)

    已知：⊙O1与⊙O2相交于点A、B，过点B作CD⊥AB，分别交⊙O1和⊙O2于点C、D．
    （1）如图，求证：AC是⊙O1的直径；
    （2）若AC=AD，
    ①如图，连接BO2、O1O2，求证：四边形O1C BO2是平行四边形；
    ②若点O1在⊙O2外，延长O2O1交⊙O1于点M，在劣弧
    MB
    上任取一点E（点E与点B不重合），EB的延长线交优弧
    BDA
    于点F，如图所示，连接AE、AF，则AE
     
    AB（请在横线上填上“≥、≤、＜、＞”这四个不等号中的一个）并加以证明．（友情提示：结论要填在答题卡相应的位置上）
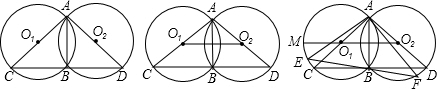
    精英家教网

    查看答案和解析>>

    已知两个等圆⊙O1和⊙O2交于A，B两点，⊙O1经过点O2，点C是上的任一点(不与A，O2，B重合)，连接BC并延长，交⊙O2于D，连接AC，AD．求证________．

    (1)操作、测量(图(1)供操作、测量用)，测量时可使用刻度尺或圆规：将图(1)按题中叙述补充完整，并观察或度量AC，AD，CD三条线段的长短，通过观察或度量，说出三条线段长短之间存在怎样的关系；

    (2)猜想结论(求证部分)，并证明你的猜想；(在你补充完整的图(1)中进行证明)

    (3)如图(2)所示，若点C是的中点，AC与O1O2交于点E，连接O1C，O2C，求证CE2＝O1O2·EO2．

    查看答案和解析>>

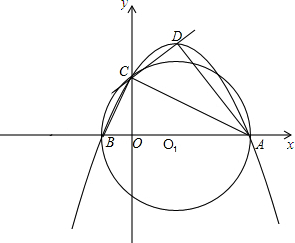    如图，在平面直角坐标系xOy中，AB在x轴上，AB=10，以AB为直径的⊙O1与y轴正半轴交于点C，连接BC、AC，CD是⊙O1的切线，AD⊥CD于点D，tan∠CAD=
    12
    ，抛物线y=ax2+bx+c过A、B、C三点．
    （1）求证：∠CAD=∠CAB；
    （2）求抛物线的解析式；
    （3）判断抛物线的顶点E是否在直线CD上，并说明理由．

    查看答案和解析>>

    如图，在平面直角坐标系xOy中，AB在x轴上，AB=10，以AB为直径的⊙O1与y轴正半轴交于点C，连接BC、AC，CD是⊙O1的切线，AD⊥CD于点D，tan∠CAD=，抛物线y=ax2+bx+c过A、B、C三点．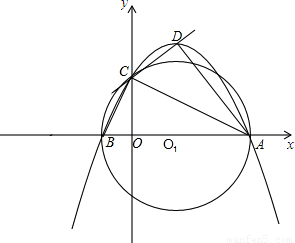
    （1）求证：∠CAD=∠CAB；
    （2）求抛物线的解析式；
    （3）判断抛物线的顶点E是否在直线CD上，并说明理由．

    查看答案和解析>>

    在等腰梯形ABCD中，AD∥BC，AB=DC，且BC=2．以CD为直径作⊙O1交AD于点Ｅ，过点Ｅ作ＥF⊥AB于点F．建立如图所示的平面直角坐标系，已知A、B两点坐标分别为A（2，0）、B（0，）．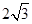
    【小题1】求C、D两点的坐标；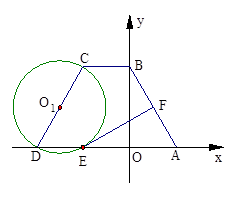

    【小题2】求证：ＥF为⊙O1的切线
    【小题3】线段CD上是否存在点P，使以点P为圆心，PD为半径的⊙P与y轴相切．如果存在，请求出P点坐标；如果不存在，请说明理由．

    查看答案和解析>>


    同步练习册答案