如图1，P为正方形ABCD内一点，且PA：PB：PC=1：2：3，求∠APB的度数．
小娜同学的想法是：不妨设PA=1，PB=2，PC=3，设法把PA、PB、PC相对集中，于是他将△BCP绕点B顺时针旋转90°得到△BAE（如图2），然后连接PE，问题得以解决．
请你回答：图2中∠APB的度数为______．
请你参考小娜同学的思路，解决下列问题：
如图3，P是等边三角形ABC内一点，已知∠APB=115°，∠BPC=125°．
（1）在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形（保留画图痕迹）；
（2）求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于______．

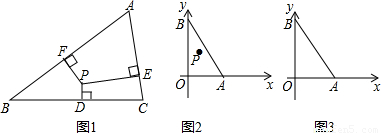
我们把三角形内部的一个点到这个三角形三边所在直线距离的最小值叫做这个点到这个三角形的距离．如图1，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，如果PE≥PF≥PD，则称PD的长度为点P到△ABC的距离.如图2、图3，在平面直角坐标系中，已知A（6，0），B（0，8），连接AB.

（1）若P在图2中的坐标为（2，4），则P到OA的距离为      ，P到OB的距离为      ，P到AB的距离为     ，所以P到△AOB的距离为      ；

（2）若点Q是图2中△AOB的内切圆圆心，求点Q到△AOB距离的最大值；

（3）若点R是图3中△AOB内一点，且点R到△AOB的距离为1，请画出所有满足条件的点R所形成的封闭图形，并求出这个封闭图形的周长.（画图工具不限）

	（第23题图1）                （第23题图2）               （第23题图3）