练习册

  • 练习册
  • 试题
    (1)由△PCD为等边三角形.故∠PCD＝∠PDC＝60 o.从而∠ACP＝∠PBD=120 o,若要△ACP∽△PDB.必要.从而 AC·DB＝PC·PD.又PC＝PD＝CD.故CD2＝AC·DB,(2)由△PDB∽△ACD.所以∠A＝∠DPB.∠APC＝∠B.又因为∠A+∠APC+ACP＝180o.故∠A+∠APC＝60o.又∠CPD＝60o.故∠APB＝∠APC+∠BPD+∠CPD=120o 【查看更多】

     

    题目列表(包括答案和解析)

    勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=6，AC=8，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为
    440
    440
    ．

    查看答案和解析>>

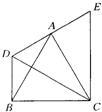    21、如图所示，△ABC为等边三角形，以AB为边向外作△ABD，使∠ADB=120°，然后把△BCD绕着点C按顺时针方向旋转60°得到△ACE，如图所示，已知BD=5，AD=3．
    （1）由旋转可知线段BC，CD，BD的对应线段分别是什么？
    （2）求∠DAE的度数；
    （3）求∠BDC的度数；
    （4）求CE的长．

    查看答案和解析>>

    已知：抛物线y=x2-（2m+4）x+m2-10与x轴交于A、B两点，C是抛物线的顶点．
    （1）用配方法求顶点C的坐标（用含m的代数式表示）；
    （2）“若AB的长为2
    		2
    ，求抛物线的解析式．”解法的部分步骤如下，补全解题过程，并简述步骤①的解题依据，步骤②的解题方法；
    解：由（1）知，对称轴与x轴交于点D（
     
    ，0）
    ∵抛物线的对称性及AB=2
    		2
    ，
    ∴AD=DB=|xA-xD|=2
    		2
    ．
    ∵点A（xA，0）在抛物线y=（x-h）2+k上，
    ∴0=（xA-h）2+k①
    ∵h=xC=xD，将|xA-xD|=
    		2
    代入上式，得到关于m的方程0=(
    		2
    )2+(      )    ②
    （3）将（2）中的条件“AB的长为2
    		2
    ”改为“△ABC为等边三角形”，用类似的方法求出此抛物线的解析式．

    查看答案和解析>>

    下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第5个图案中白色正方形的个数为（　　）

    查看答案和解析>>

    下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第8个图案中白色正方形的个数为（　　）

    查看答案和解析>>


    同步练习册答案