题目列表(包括答案和解析)
如果方程ax2+5=(x+2)(x－1)是关于x的一元二次方程，则a__________.
对于关于x的一元二次方程ax2＋bx＋c＝0(a≠0)，如果a＋b＋c＝0，那么它的两个根分别为x1＝1，x2＝
．说明如下：
由于a＋b＋c＝0，则c＝－a－b
将c＝－a－b代入原方程，得ax2＋bx－a－b＝0．
即a(x2－1)＋b(x－1)＝0，所以(x－1)(ax＋a＋b)＝0
解得x1＝1，x2＝
．
请利用上面推导出来的结论，快速求解下列方程：
(1)3x2－5x＋2＝0，x1＝________，x2＝________；
(2)7x2－4x－3＝0，x1＝________，x2＝________；
(3)13x2＋7x－20＝0，x1＝________，x2＝________；
(4)x2－(
＋1)x＋＝0，x1＝________，x2＝________；
(5)2004x2－2003x－1＝0，x1＝________，x2＝________；
(6)(b－c)x2＋(c－a)x＋(a－b)＝0(b≠c)，x1＝________，x2＝________；
(7)请你写出3个一元二次方程，使它们都有一个根是1．
若x1、x2是关于一元二次方程ax2＋bx＋c(a≠0)的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1＋x2＝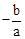
，x1•x2＝
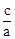．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝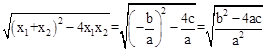
。
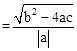参考以上定理和结论，解答下列问题：
设二次函数y＝ax2＋bx＋c(a＞0)的图象与x轴的两个交点A(x1，0)，B(x2，0)，抛物线的顶点为C，显然△ABC为等腰三角形．
(1)当△ABC为直角三角形时，求b2－4ac的值；
(2)当△ABC为等边三角形时，求b2－4ac的值．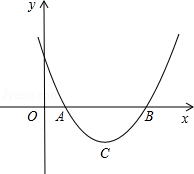
若x1、x2是关于一元二次方程ax2＋bx＋c(a≠0)的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1＋x2＝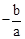
，x1•x2＝
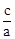．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝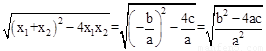
。
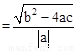参考以上定理和结论，解答下列问题：
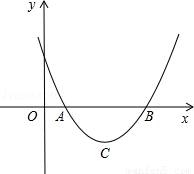
设二次函数y＝ax2＋bx＋c(a＞0)的图象与x轴的两个交点A(x1，0)，B(x2，0)，抛物线的顶点为C，显然△ABC为等腰三角形．
(1)当△ABC为直角三角形时，求b2－4ac的值；
(2)当△ABC为等边三角形时，求b2－4ac的值．
，x1﹒x2＝
．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：
＝
＝
＝
．
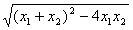0)的图象与x轴的两个交点A(x1，0)、B(x2，0)，抛物线的顶点为C，显然△ABC为等腰三角形．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com