
题目列表(包括答案和解析)
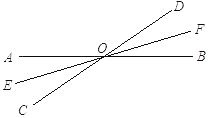 OC=30°,求∠EOF.
OC=30°,求∠EOF.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 22、(A类)如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求OE的长.
22、(A类)如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求OE的长.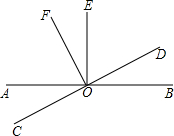 如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,求∠EOF的度数.
如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,求∠EOF的度数. 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com