练习册

  • 练习册
  • 试题
    4．如图.在Rt△ABC中.AB＝AC.D.E是斜边BC上两点.且∠DAE＝45°.将△ADC绕点A顺时针90°旋转后.得到△AFB.连接EF．下列结论中正确的个数有 ①∠EAF＝45°,②△ABE∽△ACD,③EA平分∠CEF,④BE2+DC2＝DE2 A．1个 B．2个 C．3个 D．4个 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：

    ①△AED≌△AEF；

    ②BE＋DC＝DE；

    ③BE2＋DC2＝DE2．其中正确的有

    [　　]

    A．1个

    B．2个

    C．3个

    D．4个

    查看答案和解析>>

    如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：

    ①△AED≌△AEF；

    ②△ABE∽△ACD；

    ③BE＋DC＝DE；

    ④BE2＋DC2＝DE2

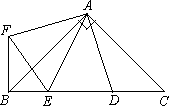
    其中正确的是

    [　　]

    A．②④；

    B．①④；

    C．②③；

    D．①③．

    查看答案和解析>>

    如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：

    ①△AED≌△AEF；

    ②△ABE∽△ACD；

    ③BE＋DC＝DE；

    ④BE2＋DC2＝DE2

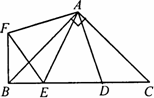
    以上结论中，一定正确的是

    [　　]
    A．

    ①④

    B．

    ②④

    C．

    ②③

    D．

    ①③

    查看答案和解析>>

    如图，在Rt△ABC中，∠ACB＝，BC＞AC，以斜边AB所在直线为x轴，以斜边AB上的高所在直线为y轴，建立直角坐标系，若OA2＋OB2＝17，且线段OA、OB的长度是关于x的一元二次方程x2－mx＋2(m－3)＝0的两个根．

    (1)求C点的坐标；

    (2)以斜边AB为直径作圆与y轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图；

    (3)在抛物线上是否存在点P，使△ABP与△ABC全等？若存在，求出符合条件的P点的坐标；若不存在，说明理由．

    查看答案和解析>>

    如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=450，将△ADC绕点A顺时针旋转900后，得到△AFB，连接ＥＦ，下列结论：（１）△ＡＥＤ≌△ＡＥＦ；（２）△ＡＢＥ∽△ＡＣＤ；（３）ＢＥ＋ＤＣ＝ＤＥ；（４）ＢＥ２＋ＤＣ２＝ＤＥ２．其中正确的是（　　　）

    Ａ．（2）（4）       B.（1）(4 )      C. (2 )  (3 )      D. (1 )   (3 )

    查看答案和解析>>


    同步练习册答案