
题目列表(包括答案和解析)
在一元二次方程口![]() 0中,如果
0中,如果![]() ≥0,那么它的两个实数根是
≥0,那么它的两个实数根是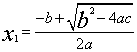 ,
,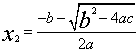 .
.
通过计算可得![]() ,
,![]() .
.
由此可见,一元二次方程的两个实数根的和与积是由一元二次方程的系数确定的.
运用上述关系解答下列问题:
(1)设方程![]() 的两个实数根分别为
的两个实数根分别为![]() 、
、![]() ,则
,则![]() +
+![]() =_________,
=_________,![]() ·
·![]() =_________.
=_________.
(2)求方程![]() 与方程
与方程![]() 所有实数根的和.
所有实数根的和.
解一元二次方程的思路是:将一元二次方程化为________方程,即降次.解一元二次方程一般解法有________,________,________.其中配方法和公式法适用于所有一元二次方程,分解因式法只适用于一些特殊的一元二次方程.
 )7+(
)7+( )7
)7 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com