阅读材料:
(1)等高线概念:在地图上,我们把地面上海拔高度相同的点连成的闭合曲线叫等高线,
例如,如图1,把海拔高度是50米,100米,150米的点分别连接起来,就分别形
成50米,100米,150米三条等高线.
(2)利用等高线地形图求坡度的步骤如下:(如图2)
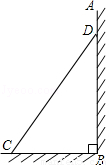
步骤一:根据两点A,B所在的等高线地形图,分别读出点A,B的高度;A,B两点的
铅直距离=点A,B的高度差;
步骤二:量出AB在等高线地形图上的距离为d个单位,若等高线地形图的比例尺为
1:m,则A,B两点的水平距离=dn;
步骤三:AB的坡度=

=

;
请按照下列求解过程完成填空.
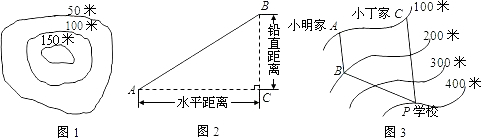
某中学学生小明和小丁生活在山城,如图3,小明每天上学从家A经过B沿着公路AB,BP到学校P,小丁每天上学从家C沿着公路CP到学校P.该山城等高线地形图的比例尺为:1:50000,在等高线地形图上量得AB=1.8厘米,BP=3.6厘米,CP=4.2厘米
(1)分别求出AB,BP,CP的坡度(同一段路中间坡度的微小变化忽略不计);
(2)若他们早晨7点同时步行从家出发,中途不停留,谁先到学校?(假设当坡度在

到

之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在

到

之间
时,小明和小丁步行的平均速度均约为1米/秒)
解:(1)AB的水平距离=1.8×50000=90000(厘米)=900(米),AB的坡度=

=

;
BP的水平距离=3.6×50000=180000(厘米)=1800(米),BP的坡度=

=

;
CP的水平距离=4.2×50000=210000(厘米)=2100(米),CP的坡度=______.
(2)因为

<

<

,所以小明在路段AB,BP上步行的平均速度均约为1.3米/秒,因为
______,所以小丁在路段CP上步行的平均速度约为______米/秒,斜坡AB的距离=

=906(米),斜坡BP的距离=
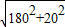
=1811(米),斜坡CP的距离=

=2121(米),所以小明从家道学校的时间=
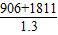
=2090(秒).小丁从家到学校的时间约为______秒.因此,______先到学校.


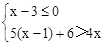 并把解集在数轴上表示出来;
并把解集在数轴上表示出来;

 =
= ;
; 到
到 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在
之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在 到
到 之间
之间 =
= ;
; =
= ;
; <
< <
< ,所以小明在路段AB,BP上步行的平均速度均约为1.3米/秒,因为
,所以小明在路段AB,BP上步行的平均速度均约为1.3米/秒,因为 =906(米),斜坡BP的距离=
=906(米),斜坡BP的距离=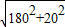 =1811(米),斜坡CP的距离=
=1811(米),斜坡CP的距离= =2121(米),所以小明从家道学校的时间=
=2121(米),所以小明从家道学校的时间=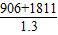 =2090(秒).小丁从家到学校的时间约为______秒.因此,______先到学校.
=2090(秒).小丁从家到学校的时间约为______秒.因此,______先到学校.