
题目列表(包括答案和解析)
(本题满分12分)
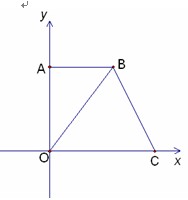
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为![]() 秒(
秒(![]() ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的![]() ?若存在,求出
?若存在,求出![]()
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求![]() 的值或
的值或![]() 的取值范围
的取值范围
 秒(
秒(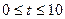 ),
),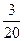 ?若存在,求出
?若存在,求出
 的值或
的值或 的取值范围
的取值范围(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,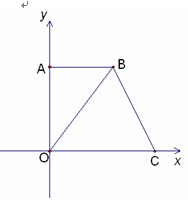
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为 秒(
秒(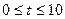 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的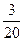 ?若存在,求出
?若存在,求出
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求 的值或
的值或 的取值范围
的取值范围
(本题满分12分) 如图,在平面直角坐标系中,抛物线与x轴交于点A、B
(点A在点B的左侧),与y轴交于点C(0,4),顶点为(1,).
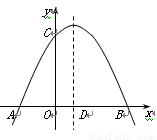
(1)求抛物线的函数解析式;
(2)抛物线的对称轴与x轴交于点D,点P在对称轴上且使△CDP为等腰三角形.请直接写出满足条件的所有点的坐标P;
(3)若点E是线段AB上的一个动点(与点A、B不重合),连接AC、BC,过点E作EF∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,请求出S的最大值及此时点E的坐标;若不存在,请说明理由.
(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,

(1) 求点B的坐标;
(2)
点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为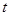 秒(
秒(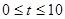 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的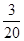 ?若存在,求出
?若存在,求出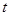
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求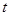 的值或
的值或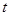 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com