练习册

  • 练习册
  • 试题
    如图.在△ABC和△DEF中.∠A=∠D.AC=DF.若根据 “ASA 说明△ABC≌△DEF.则应添加条件 = . 或 ∥ . 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在△ABC和△DEF中，∠A＝∠D，AC＝DF，若添加条件________＝________或________∥________，则可根据角边角条件得到△ABC≌△DEF；若添加条件________＝________或________∥________，则可根据角角边条件得到△ABC≌△DEF，若添加条件________＝________，则可根据边角边条件，得到△ABC≌△DEF．

    查看答案和解析>>

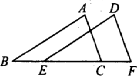
    如图（八），在△ABC和△DEF中，∠A=∠D，AC=DF，若根据“ASA”说明△ABC≌△DEF，则应添加条件      =        .    或      ∥       .

    查看答案和解析>>

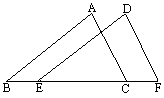
    如图所示是操场上坚立的旗杆AB和它在太阳光下的影子AC，以及一棵小树DE．

    (1)根据旗杆AB的影子AC．请画出小树DE此刻在太阳光下的影子DF．并说明理由．

    (2)在1的条件下．如图所示中的△ABC和△DEF是什么关系？为什么？

    (3)若量得小树高DE＝2m，其影长DF＝3m．旗杆的影长AC＝9m．求旗杆的高．

    查看答案和解析>>

    如图，在△ABC和△DEF中，∠A＝∠D，AC＝DF，若添加条件________＝________或________∥________，可根据角边角条件说明△ABC≌△DEF；若添加条件________＝________或________∥________，则可根据角角边条件得到△ABC≌△DEF；若添加条件________＝________，则可根据边角边条件，得到△ABC≌△DEF

    查看答案和解析>>


    【问题提出】
    学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
    【初步思考】
    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    【深入探究】
    第一种情况：当∠B是直角时，△ABC≌△DEF．
    （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据       ，可以知道Rt△ABC≌Rt△DEF．
    第二种情况：当∠B是钝角时，△ABC≌△DEF．
    （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
    （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
    （4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若       ，则△ABC≌△DEF．

    查看答案和解析>>


    同步练习册答案