
题目列表(包括答案和解析)
(本小题满分10分)在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为![]() (0°<
(0°<![]() <180°),得到△A1B1C.
<180°),得到△A1B1C.

(1)如图1,当AB∥CB1时,设A1B1与BC相交于点D.证明:△A1CD是等边三角形;
(2)如图2,连接AA1、BB1,设△ACA1和△BCB1的面积分别为S1、S2.
求证:S1∶S2=1∶3;
(3)如图3,设AC的中点为E,A1B1的中点为P,AC=a,连接EP.当![]() 等于多少度时,EP的长度最大,最大值是多少?
等于多少度时,EP的长度最大,最大值是多少?
 (0°<
(0°< <180°),得到△A1B1C.
<180°),得到△A1B1C.
 等于多少度时,EP的长度最大,最大值是多少?
等于多少度时,EP的长度最大,最大值是多少?
 和
和 ,且
,且 到AB、BC、AD的距离与
到AB、BC、AD的距离与 到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,清说明理由.
到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,清说明理由. ,直线y=
,直线y= 经过点C,交y轴于点G。
经过点C,交y轴于点G。
 上且经过点C、D的抛物
上且经过点C、D的抛物 平移,平移后
平移,平移后 (本小题满分12分)
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=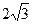 ,直线y=
,直线y=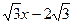 经过点C,交y轴于点G。
经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=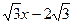 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
(3)将(2)中的抛物线沿直线y=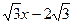 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com