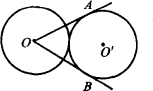圆的滚动问题探索:
(1)如图1,一个半径为r的圆沿直线方向从A地滚动到B地,若AB的长为m,则该圆在滚动过程中自转了______圈.(用含的式子表示)
试验:
现有两个半径相等的圆(如图5),将⊙O
2固定,⊙O
1沿定圆的周围滚动,滚动时两圆保持相外切的位置关系.当⊙O
1沿⊙O
2周围滚动一周回到原来的位置时,⊙O
1自转了2圈,而⊙O
1的圆心运动的线路也是一个圆,而这个圆的周长恰好是⊙O
1的周长的2倍.
(2)如图2,⊙O
1的半径为r,⊙O
2的半径为R(R>r),现将⊙O
2固定,让,⊙O
1沿⊙O
2的周围滚动,滚动时两圆保持相外切的位置关系.当⊙O
1沿⊙O
2沿周围滚动一周回到原来的位置时,⊙O
1自转了______圈;

(3)如图3,⊙O
1,和⊙O
2内切,⊙O
1的半径为r,⊙O
2的半径为R(R>r),现将⊙O
2固定,让,⊙O
1沿⊙O
2的边缘滚动,动时两圆保持相内切的位置关系.当⊙O
1沿⊙O
2边缘滚动一圈回到原来的位置时,⊙O
1自转了______圈.
解决问题:
如图4,一个等边三角形与它的一边相切的圆的周长相等,当此圆按箭头方向从某一位置沿等边三角形的三边作无滑动滚动,直至回到原来的位置时,该圆自转了多少圈?请说明理由.


![]() 相外切,过O作⊙
相外切,过O作⊙![]() 的两条切线OA、OB,A、B是切点,则∠AOB等于多少?
的两条切线OA、OB,A、B是切点,则∠AOB等于多少?